Cube root - practice problems
Number of problems found: 204
- Cbrt of fraction
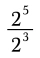 If a fraction is multiplied by itself and then divided by the reciprocal of the same fraction, the result is 18 26/27. Find the fraction.
If a fraction is multiplied by itself and then divided by the reciprocal of the same fraction, the result is 18 26/27. Find the fraction. - Binary series
 The 4th term of a G.P. is 16 and the 7th term is 128 . Find the first term and common ratio of the series.
The 4th term of a G.P. is 16 and the 7th term is 128 . Find the first term and common ratio of the series. - Ones cube
 Find the volume of a cube whose total surface area is 6 m².
Find the volume of a cube whose total surface area is 6 m². - Geometric 20
 Find the geometric mean of 15 15 20 25 30.
Find the geometric mean of 15 15 20 25 30. - Perfect square or cube
 Would you classify 324 as a perfect square, perfect cube, both, or neither? ...
Would you classify 324 as a perfect square, perfect cube, both, or neither? ... - A chest made
 A chest in the shape of a cuboid made of sheet iron has dimensions of 24 m 0.8 m and 0.5 m. What will be the volume of a chest in the shape of a cube with the same surface area?
A chest in the shape of a cuboid made of sheet iron has dimensions of 24 m 0.8 m and 0.5 m. What will be the volume of a chest in the shape of a cube with the same surface area? - Two cubes 3
 Two cubes modeled from plasticine have single-digit integer edge lengths with a difference of 1 cm. Can one large cube with an integer edge length be modeled from the same amount of plasticine?
Two cubes modeled from plasticine have single-digit integer edge lengths with a difference of 1 cm. Can one large cube with an integer edge length be modeled from the same amount of plasticine? - Box
 A paper box is in the shape of a cube. 2,400 cm² of paper was used to make it. Bends for gluing the walls are not included. Calculate the volume of the box.
A paper box is in the shape of a cube. 2,400 cm² of paper was used to make it. Bends for gluing the walls are not included. Calculate the volume of the box. - Original model
 When drying, the modeling mass loses 36% of its original volume. If the cube's volume is 5.12 dm³ after drying, what was the original length of the edge?
When drying, the modeling mass loses 36% of its original volume. If the cube's volume is 5.12 dm³ after drying, what was the original length of the edge? - Calculate 83044
 The cube comprises 64 small cubes, each with an edge length of 15 mm. Calculate the wall length and body diagonals.
The cube comprises 64 small cubes, each with an edge length of 15 mm. Calculate the wall length and body diagonals. - Cube-shaped 82606
 The paper box is cube-shaped. 2400 cm² was used for its production. Bends for gluing the walls are omitted. What is the volume of the box?
The paper box is cube-shaped. 2400 cm² was used for its production. Bends for gluing the walls are omitted. What is the volume of the box? - ABCDEFGH 82499
 In the cube ABCDEFGH, the area of triangle ABK is √20 cm². How much cm² is the volume of ABGH in a cube if you know that K is the midpoint of edge CG?
In the cube ABCDEFGH, the area of triangle ABK is √20 cm². How much cm² is the volume of ABGH in a cube if you know that K is the midpoint of edge CG? - Diagonal of a cube
 Calculate the volume of a cube with a wall diagonal of u = 20 cm.
Calculate the volume of a cube with a wall diagonal of u = 20 cm. - Calculate 82077
 The surface of the cube is 150 dm². Calculate its volume.
The surface of the cube is 150 dm². Calculate its volume. - Increases 81991
 What % of bacteria will increase hourly if the number increases from 100,000 to 370,000 in 5 hours?
What % of bacteria will increase hourly if the number increases from 100,000 to 370,000 in 5 hours? - Inscribed cube
 A cube is inscribed in a sphere with a radius of 27 cm. Calculate its volume and surface area.
A cube is inscribed in a sphere with a radius of 27 cm. Calculate its volume and surface area. - Circumscribed - sphere
 A cube with a volume of 4096 cm³ is described and inscribed by a sphere. Calculate how many times the volume of the circumscribed sphere is greater than the inscribed sphere.
A cube with a volume of 4096 cm³ is described and inscribed by a sphere. Calculate how many times the volume of the circumscribed sphere is greater than the inscribed sphere. - Expressed 79474
 The length of the cube's edge in cm is expressed as a natural number. Its volume is greater than 100 and less than 200. Calculate the surface area of the cube.
The length of the cube's edge in cm is expressed as a natural number. Its volume is greater than 100 and less than 200. Calculate the surface area of the cube. - Smallest 79434
 Find the smallest natural x such that 2x is the square and 3x is the third power of a natural number.
Find the smallest natural x such that 2x is the square and 3x is the third power of a natural number. - Calculate 78514
 The block has a length of 12 cm and a width of 0.6 dm. The height is the same size as the edge of a cube whose volume is 64cm³. Calculate the volume of the cuboid in cm³.
The block has a length of 12 cm and a width of 0.6 dm. The height is the same size as the edge of a cube whose volume is 64cm³. Calculate the volume of the cuboid in cm³.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
