Perfect square or cube
You need to know the following knowledge to solve this word math problem:
algebraarithmeticsolid geometryplanimetricsnumbersUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Perfect cube
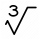Which of the following numbers is not a perfect cube? a. 64 b. 729 c. 800 d. 1331 - Perfect cubes
Suppose a number is chosen at random from the set (0,1,2,3,. .. ,202). What is the probability that the number is a perfect cube? - Percentage 3547
Quality control found that out of 4,200 products, 3,074 were perfect. What percentage did the scraps represent? - Pentagonal pyramid
Find the volume and surface of a regular pentagonal pyramid with a base edge a = 12.8 cm and a height v = 32.1 cm. - Rainfall
The annual average rainfall in India was 26 461 mm in Cherrapunji in 1981. How many hectoliters of water fell on one square meter? Would you fit this amount of water into a cube of three meters? - Root
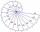Use the law of square roots: cbrt (sqrt[2] (sqrt[4] (6))) = sqrt[n] (6) - QuizQ2
The square of the first number is equal to three-fifths of the second number. Determine both numbers if you know that the second number is five times greater than the first, and neither of the numbers is not equal to zero.
