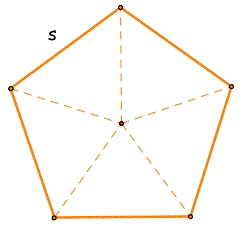
Pentagonal pyramid
Find the volume and surface of a regular pentagonal pyramid with a base edge a = 12.8 cm and a height v = 32.1 cm.
Final Answer:
Showing 2 comments:
Sebf
I think we should see all the variables, I mean : a, v, n S1, S2 and all the things used to finally get the result S. On the scheme.
I understand the way you calculate on your savant literature. But I 'm sure i' m not the only one who would like to learn about this science visually.
For me it's OK. But I cannot share that.
Very sad while it is very clever.
Please explain how you get the result visually on the scheme.
Thanks by advance
Regards
I understand the way you calculate on your savant literature. But I 'm sure i' m not the only one who would like to learn about this science visually.
For me it's OK. But I cannot share that.
Very sad while it is very clever.
Please explain how you get the result visually on the scheme.
Thanks by advance
Regards
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
See also our right triangle calculator.
See also our right triangle calculator.
You need to know the following knowledge to solve this word math problem:
algebrasolid geometryplanimetricsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Pentagonal pyramid
The height of a regular pentagonal pyramid is as long as the edge of the base, 20 cm. Calculate the volume and surface area of the pyramid. - Calculate 4S pyramid
Calculate the surface area and volume of a regular 4-sided pyramid with a base edge of a = 12 cm and a height of v = 5 cm. - Quadrilateral pyramid Find the height and surface of a regular quadrilateral pyramid with a base edge a = 8cm and a wall height w = 10cm. Sketch a picture.
- Surface of pyramid
A regular quadrilateral pyramid has the height of the sidewall equal to the length of the edge of the base. The area of the sidewall is 32 cm². What is the surface of the pyramid? - Triangular pyramid
Calculate the volume and surface area of a regular triangular pyramid with a height equal to the base edge, which is 10 cm long. - Hexagonal pyramid
Calculate the volume and the surface of a regular hexagonal pyramid with a base edge length of 3 cm and a height of 5 cm. - Special body
Above each wall of a cube with an edge a = 30 cm, we construct a regular quadrilateral pyramid with a height of 15 cm. Find the volume of the resulting body.
