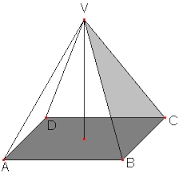
Quadrilateral pyramid
We have a regular quadrilateral pyramid with a base edge a = 10 cm and a height v = 7 cm.
Calculate
1/base area
2/casing area
3/pyramid surface
4/volume of the pyramid
Your answer:
Calculate
1/base area
2/casing area
3/pyramid surface
4/volume of the pyramid
Your answer:
Tips for related online calculators
See also our right triangle calculator.
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
solid geometryplanimetryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Quadrilateral pyramid
A regular quadrilateral pyramid has a volume of 24 dm³ and a base edge a = 4 dm. Calculate: a/height of the pyramid b/sidewall height c/surface of the pyramid - Quadrilateral pyramid
Calculate the surface area and volume of a regular quadrilateral pyramid whose base edge is 5 cm long and whose height is 10 cm. - Pyramid Height and Surface
Calculate the height and surface of a regular quadrilateral pyramid with a base edge a = 8 cm and a wall height w = 10 cm. - Quadrilateral pyramid
A quadrilateral pyramid has a rectangular base with 24 cm and 13 cm dimensions. The height of the pyramid is 18 cm. Calculate: 1/the area of the base 2/casing area 3/pyramid surface 4/volume of the pyramid - Pyramid surface height The regular quadrilateral pyramid has a volume of 212 m³ and a base edge a = 7.2 m. Calculate the surface area and height of the pyramid.
- Quadrilateral pyramid
Find the height and surface of a regular quadrilateral pyramid with a base edge a = 8 cm and a wall height w = 10 cm. Sketch a picture. - Pyramid 4sides
Calculate the volume and the surface of a regular quadrilateral pyramid when the edge of the base is 4 cm long, and the pyramid's height is 7 cm.
