Isolating a variable in the formula - math word problems - page 22 of 145
Number of problems found: 2889
- Difference 81835
 Determine the difference d in AP if a1=3 and a1+a2=12
Determine the difference d in AP if a1=3 and a1+a2=12 - Understanding 81807
 The aquarium is 0.7m long and 25cm wide. The battery is deep if it can hold no more than 87.5 liters of water. I need help understanding how to calculate this.
The aquarium is 0.7m long and 25cm wide. The battery is deep if it can hold no more than 87.5 liters of water. I need help understanding how to calculate this. - Arithmetic 81798
 Two arithmetic sequences have the same first term. The nth term of the first sequence is 15, and of the second sequence, 21. The sum of the first n terms of the first sequence is 63, and of the second sequence, 84. Write the sums of the first n terms of b
Two arithmetic sequences have the same first term. The nth term of the first sequence is 15, and of the second sequence, 21. The sum of the first n terms of the first sequence is 63, and of the second sequence, 84. Write the sums of the first n terms of b - Descending 81797
 The sum of the first two terms of the descending geometric sequence is five quarters, and the sum of the infinite geometric series formed from it is nine quarters. Write the first three terms of the geometric sequence.
The sum of the first two terms of the descending geometric sequence is five quarters, and the sum of the infinite geometric series formed from it is nine quarters. Write the first three terms of the geometric sequence. - Determine 81794
 Determine the quotient of the geometric sequence with the first term a1=36 so that s2 is less than or equal to 252.
Determine the quotient of the geometric sequence with the first term a1=36 so that s2 is less than or equal to 252. - Calculate 81757
 Calculate the size of the largest angle in triangle ABC if a = 7 cm, b = 8 cm, and c = 13 cm. Calculate the area of the triangle, the height per side a.
Calculate the size of the largest angle in triangle ABC if a = 7 cm, b = 8 cm, and c = 13 cm. Calculate the area of the triangle, the height per side a. - Determine 81756
 The area for shooting training has the shape of a trapezoid, the parallel sides of which are 36m, 21m long, and the remaining sides are 14m, 16m long. Determine the size of the interior angles with a longer base.
The area for shooting training has the shape of a trapezoid, the parallel sides of which are 36m, 21m long, and the remaining sides are 14m, 16m long. Determine the size of the interior angles with a longer base. - Calculate 81743
 Calculate the size of the other side of the rectangle if the size of one of its sides is 90m and the area is 3600 m².
Calculate the size of the other side of the rectangle if the size of one of its sides is 90m and the area is 3600 m². - Coefficient 81704
 In the equation of the line p: ax-2y+1=0, determine the coefficient a so that the line p: a) it formed an angle of 120° with the positive direction of the x-axis, b) passed through point A[3,-2], c) was parallel to the x-axis, d) had a direction of k = 4.
In the equation of the line p: ax-2y+1=0, determine the coefficient a so that the line p: a) it formed an angle of 120° with the positive direction of the x-axis, b) passed through point A[3,-2], c) was parallel to the x-axis, d) had a direction of k = 4. - Block-shaped 81632
 The block-shaped pool is 40 meters long and 18 meters wide. Ten thousand eight hundred hectoliters of water were poured into it. How high is the water in it (how deep is the pool)?
The block-shaped pool is 40 meters long and 18 meters wide. Ten thousand eight hundred hectoliters of water were poured into it. How high is the water in it (how deep is the pool)? - Dimensions 81608
 Find out if a circle with a volume of 38.5 cm² fits into a rectangle with dimensions of 110 mm and 65 mm.
Find out if a circle with a volume of 38.5 cm² fits into a rectangle with dimensions of 110 mm and 65 mm. - Rectangle's 81596
 The rectangle has a perimeter of 30 cm. The ratio of its sides a: b=2:3. Calculate the sides' lengths and the rectangle's area.
The rectangle has a perimeter of 30 cm. The ratio of its sides a: b=2:3. Calculate the sides' lengths and the rectangle's area. - Intersection 81594
 Given a trapezoid ABCD and the sizes of the interior angles. Angle SDC 32° SAD angle 33° SDA angle 77° Angle CBS 29°, where S is the intersection of the diagonals. What is the size of the angle BSA?
Given a trapezoid ABCD and the sizes of the interior angles. Angle SDC 32° SAD angle 33° SDA angle 77° Angle CBS 29°, where S is the intersection of the diagonals. What is the size of the angle BSA? - Determine 81587
 Determine the type of polygon if the number of all diagonals is 90. (Write down the number of its pages.)
Determine the type of polygon if the number of all diagonals is 90. (Write down the number of its pages.) - Calculate 81560
 The cone's surface is 75.36 cm, and the radius is 3 cm. Calculate the volume of the cone.
The cone's surface is 75.36 cm, and the radius is 3 cm. Calculate the volume of the cone. - Three ratios
 Calculate x in terms of: x:7=6:4 1/2:x=5:3/4 4:3=8:x
Calculate x in terms of: x:7=6:4 1/2:x=5:3/4 4:3=8:x - Spherical 81527
 Sketch a spherical layer formed from a sphere with a radius of r= 8.5cm, given: v=1.5cm, r1=7.7cm, r2=6.8cm. What is its volume?
Sketch a spherical layer formed from a sphere with a radius of r= 8.5cm, given: v=1.5cm, r1=7.7cm, r2=6.8cm. What is its volume? - Cylinder-shaped part
 A truncated cone-shaped part with base radii of 4 cm and 22 cm is to be recast into a cylinder-shaped part of the same height as the original part. What base radius will the new part have?
A truncated cone-shaped part with base radii of 4 cm and 22 cm is to be recast into a cylinder-shaped part of the same height as the original part. What base radius will the new part have? - Archaeologists
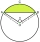 Archaeologists need to find out the size of the vessel if the sherd found was in the shape of a circular section with a length of 12 cm and a height of 3 cm. What is the area of this section?
Archaeologists need to find out the size of the vessel if the sherd found was in the shape of a circular section with a length of 12 cm and a height of 3 cm. What is the area of this section? - Times 81462
 5 to -11 times 5 to -7/5 to zero times 5 to -15 minus ( -5 ) to -2
5 to -11 times 5 to -7/5 to zero times 5 to -15 minus ( -5 ) to -2
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
