Examples for secondary school students

I enjoyed high school math the most. It was faster paced, more complex, and overall more in-depth. It wasn't just mechanical multiplication tables like in elementary school. They even took derivatives and integrals.

Number of problems found: 4611

Two terms and d
The 8th term of an AP is 17 and its 14th term is 29. Find the common difference of the AP.
Common work 2
Person A works twice as fast as person B. If both of them can together finish a piece of work in 12 days then person B alone can do it in how many days?
Three legs journey
A train runs for 3 h at the speed of 40 km/h and then for 4.5 h at the speed of 60 km/h.Thus it covers 3/5th part of the whole distance. It wants to cover the remaining distance in 4 h, find the average speed of the train for remaining distance.
ABCD rhombus
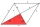ABCD is a rhombus with sides 10.5cm. If the length of the diagonal AC=15.8cm, using cosine formula. a. calculate the length of the diagonal BD correct to the nearest cm b. the angles of the rhombus to the nearest degree.
Spherical sector - parameters
Find the volume and surface area of spherical sector whose base has an altitude of 8cm. Drawn on a sphere whose diameter is 36 cm.
Insert two > GP
If 4, 36, 324 are in the geometric progression (GP) insert two more numbers in this progression so that it again forms a GP.
According 10
According to the Board of Math Examiners, approximately 62% of people taking the Math Exam passed the exam. If 18 people who have taken the Math Exam are randomly selected, what is the probability that at least 76% have passed? Round your answer to 4 deci
Common difference 4
The 28th term of an AP is -5. Find its common difference if its first term is 31.
Vertical components
Find the horizontal and vertical components of the vector which has magnitude 750 as shown in the following figure.
Angle of elevation 3
The angle of elevation of a pole from a point on the horizontal ground is 15°. After going up a distance of 10m towards the pole the angle of elevation became 30°.What is the height of the pole?
V jedálni
V školskej jedálni ZŠ urobili prieskum medzi žiakmi, ktoré jedlo im najviac chutí. Výsledky vyjadruje prvotná tabuľka: Palacinky; 102 Vyprážaný syr; 81 Špagety ; 18 Dukátové buchtičky ; 42 Kura s ryžou ; 30 Určte, čo je: štatistický súbor, štatistickú jed
Journey 9
A person covers half of his journey at 40 km/h and rest of his 20 km/h. Find his average speed of the whole journey.
Lamp shade
A lamp shade is in the form of a frustum of a cone with slant height 7 in., radii of bases 3 in. and 7 in. respectively. How much material is used in its construction if ¼ in. is allowed for the seam.
Area + perimeter TR2
Find the area of a triangle, two sides of which are 8 cm and 11 cm and the perimeter is 32 cm.
GP - negative term
The first term of a GP is -3 and the square of the second term is equal to its 4th term. Find the 7th term of the GP.
Mother and daughter 6
A mother is six time as old as her daughter. In 6 years time she will be four times as old as her daughter . How old is each of them?
Alcohol mixture 3
A mixture contains alcohol and water in the ratio 4:3. If 7 liters of water is added, the ratio of alcohol and water becomes 3:4. Find the quantity of alcohol in the mixture.
Equation of the line
Find the equation of the line through (1, 2) with slope 3.
The sum 53
The sum ofthree numbers of a GP series is 35 and their product is 1000. Find the numbers.
A train 7
A train overtakes two persons. They are walking in the same direction as the train at the rate of 2 km/hr and 4 km/hr. The train passes them completely in 9 and 10 seconds respectively. Find the length of the train.

Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.