Examples for secondary school students - page 18 of 231
Number of problems found: 4610
- Tunnel - quadrilateral
 How long will the tunnel AB be, distances AD=35 m, DC=120 m, CB=85 m, and angles ADC=105 degrees and BCD=71 degrees. ABCD is a quadrilateral.
How long will the tunnel AB be, distances AD=35 m, DC=120 m, CB=85 m, and angles ADC=105 degrees and BCD=71 degrees. ABCD is a quadrilateral. - Sale of a bill of exchange
 A businessman bought a bill of exchange 6 months before its maturity. After deducting interest at an interest rate of 10% p. . a., he paid €19,000 for it. How much € of interest was deducted from the face value of the bill?
A businessman bought a bill of exchange 6 months before its maturity. After deducting interest at an interest rate of 10% p. . a., he paid €19,000 for it. How much € of interest was deducted from the face value of the bill? - 9 rectangles
 A large rectangle is divided into 9 small rectangles. How many rectangles are there in total?
A large rectangle is divided into 9 small rectangles. How many rectangles are there in total? - Rotational motion of a cylinder
 Calculate the kinetic energy of a cylindrical body of radius r= 0.08 meter and mass m= 1.5kg at time t= 5 s, if this body rotates around an axis passing through the center of the cylinder with a constant acceleration Ԑ= 5 rad/s², if at time t=.
Calculate the kinetic energy of a cylindrical body of radius r= 0.08 meter and mass m= 1.5kg at time t= 5 s, if this body rotates around an axis passing through the center of the cylinder with a constant acceleration Ԑ= 5 rad/s², if at time t=. - Footballers 2
 Footballers have jerseys with numbers 7, 8, 9, 10, 11. The coach wants to send them to attack a) so that even jersey numbers are not next to each other b) so that odd jersey numbers are not next to each other. How many options does he have?
Footballers have jerseys with numbers 7, 8, 9, 10, 11. The coach wants to send them to attack a) so that even jersey numbers are not next to each other b) so that odd jersey numbers are not next to each other. How many options does he have? - Multiple-choice
 A multiple-choice test consists of 4 questions. Each question has three different answers, with only one answer being correct. Each question is answered randomly by one student. Determine the expected value for the number of correct answers that the stude
A multiple-choice test consists of 4 questions. Each question has three different answers, with only one answer being correct. Each question is answered randomly by one student. Determine the expected value for the number of correct answers that the stude - Physics - board, lever
 A wooden board weighing 0.5 kg is placed on a table. How much of its length can it protrude over the edge of the table without falling if a weight weighing 0.2 kg is placed at its end?
A wooden board weighing 0.5 kg is placed on a table. How much of its length can it protrude over the edge of the table without falling if a weight weighing 0.2 kg is placed at its end? - GP - free
 For a geometric sequence, an interesting relationship between the first and third terms applies: a1-a3=-1.5 a3-a1=1.5 Calculate the quotient q and the first term a1.
For a geometric sequence, an interesting relationship between the first and third terms applies: a1-a3=-1.5 a3-a1=1.5 Calculate the quotient q and the first term a1. - Equality of Moments
 A lever with a mass of 3 kg and a length of 2 m is loaded at the end with weights with masses of 5 kg and 8 kg. Find the place where the lever must be supported so that it is in balance.
A lever with a mass of 3 kg and a length of 2 m is loaded at the end with weights with masses of 5 kg and 8 kg. Find the place where the lever must be supported so that it is in balance. - 4B - truncated pyramid
 Calculate the volume of a regular truncated quadrilateral pyramid if the base edges are 10cm and 4cm and the height of the side wall is 5cm.
Calculate the volume of a regular truncated quadrilateral pyramid if the base edges are 10cm and 4cm and the height of the side wall is 5cm. - Me and my father
 My father and I are now 55 years old together. When we are 65 years old together, my father will be four times older than me. How old am I?
My father and I are now 55 years old together. When we are 65 years old together, my father will be four times older than me. How old am I? - RRL Basics
 What is the length of the smaller base of an isosceles trapezoid and the height, if a = 9 dm, the side is 6 dm and the angle ACB is 90 degrees?
What is the length of the smaller base of an isosceles trapezoid and the height, if a = 9 dm, the side is 6 dm and the angle ACB is 90 degrees? - Three dice 2
 What is the probability that two odd numbers will be the same when three dice are rolled?
What is the probability that two odd numbers will be the same when three dice are rolled? - In class 24
 There are a total of 16 students in the class, a quarter of whom are girls. We randomly select a team of five. Determine the probability that the team will have: a) at least 4 girls. b) at most 1 girl. c) no girls.
There are a total of 16 students in the class, a quarter of whom are girls. We randomly select a team of five. Determine the probability that the team will have: a) at least 4 girls. b) at most 1 girl. c) no girls. - In a regular 5
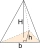 In a regular triangular prism ABCV, the deviation of the side wall and the base plane is α = 45°. Determine the deviation of the side edge and the base plane.
In a regular triangular prism ABCV, the deviation of the side wall and the base plane is α = 45°. Determine the deviation of the side edge and the base plane. - Christmas 4
 There are only 3 packages left under the tree - two for Julka and one for Zuzka. Julka took two at once. What is the probability that both belong to her?
There are only 3 packages left under the tree - two for Julka and one for Zuzka. Julka took two at once. What is the probability that both belong to her? - How many 172
 How many five-digit numbers are there that have exactly 2 fours and exactly 3 sevens in their notation?
How many five-digit numbers are there that have exactly 2 fours and exactly 3 sevens in their notation? - Between terminals
 Between terminals of a 220V resistor. A current of 220mA flows through the resistor. Determine the current that flows through the resistor if we connect it to the terminal of a 24 V voltage source.
Between terminals of a 220V resistor. A current of 220mA flows through the resistor. Determine the current that flows through the resistor if we connect it to the terminal of a 24 V voltage source. - The tower
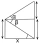 From a window 8 m above the horizontal plane, we can see the top of the tower at an elevation angle of 53 degrees 20 minutes, and its base at an angle of 14 degrees 15 minutes. How high is the tower?
From a window 8 m above the horizontal plane, we can see the top of the tower at an elevation angle of 53 degrees 20 minutes, and its base at an angle of 14 degrees 15 minutes. How high is the tower? - HAMMER 4
 Determine how many ways can the letters of the word HAMMER be rearranged so that in this rearrangement some group of consecutive letters forms the word CAL.
Determine how many ways can the letters of the word HAMMER be rearranged so that in this rearrangement some group of consecutive letters forms the word CAL.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
