Maths practice for 12-year-olds - page 52 of 362
Number of problems found: 7224
- Republican 83136
In the republican calendar (used in France from 1793 to 1805), one full day was divided into 10 hours; each hour had 100 minutes, and each minute had 100 seconds. What time would the clock show at that time when today's clock reads 15:36? - Skiing and sledding
Behind the pond, the cat Miki is skiing and Bobo is sledding down a 300-meter-long slope. Careful Bobo can go down the slope in one minute. How many km/h faster does Miki go down the hill than Bobo if he is down 20 seconds earlier? - Cylinder's 83130
Calculate the cylinder's volume if you know that the ratio of the cylinder's height to the base's radius is 3:2 and the height is 15 dm. - Christmas 83125
Parents are making Christmas gazebos/packages for children. We have 96 apples, 320 candies, 80 gum, 112 nuts. How many identical packages can I make from a given material? - Jendo's 83123
Jenda, Milan, and Tomáš have a total of 203 Pokemon cards. Jenda has twice as many cards as Tomáš, and Milan has a quarter of Jendo's number of cards. a) How many cards does Jenda have? b) How many fewer cards do Milan have than Jenda and Tomáš? - Arrangements 83122
A florist was preparing floral arrangements for a wedding. One-third of the flowers were roses, six peonies, and five-twelfth tulips; the remaining 10 were lilies. a) How many flowers did the florist use? b) How many tulips were there - Test questions
Irena solves the test. She solved three-quarters of all questions during the first reading and another sixth during the review. In total, she solved 22 questions. How many questions does the whole test consist of?
- Circumferences 83111
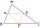Péta composed several planar shapes from mutually congruent triangles. The circumferences of the first three are 8 cm, 11.4 cm, and 14.7 cm, respectively. Determine the perimeter of the fourth shape. - Approximately 83106
The castle courtyard, with an area of 100 m², is paved with oak cubes with an edge of 8 cm. Approximately 164 bricks were used to pave m². One dm³ of oak wood weighs 0.8 kg. Calculate the weight of all the bricks used to pave the courtyard. - Friend 83103
A friend spent 2/5 on a pencil case and 3/10 on a laptop, leaving her with 3.3 euros. Thus, her total was 3.3 euros. - Notebooks 83101
Jana bought 36 notebooks, three times as many with lines as with squares notebooks. Calculate how many lined notebooks she purchased. - Solution 83099
There are spiders and flies on the window. They have a total of 38 legs. How many spiders and flies are there if a spider has 8 legs and a fly has 6? Just give one solution. - Arithmetic 83094
There were 31 students in the class, and the arithmetic average weight was 43 kg. Calculate the average weight in the class if a student weighing 91 kg has been added to the class. - Dimensions 83092
On the 1:75 scale plan, the building plot is a rectangle with 60 cm and 50 cm dimensions. If 1 m² of land costs 80 euros, what is the price of the land? - Pages 83075
The book has 500 pages. Pepa has read half as many pages as he has left. How many pages did Pep read?
- Calculate 83068
The internal volume of the barrel is 15 times greater than the bucket's volume. The volume of the bucket is 5 times the volume of the kettle. We took a third of the water from a barrel, leaving 60 liters in it. Calculate the volume of the kettle in liters - Subtract 83051
What amount will I get if I subtract 1/8 from the amount of 30000? - Rounded 83047
Mrs. Smith bought 3.15 m of fabric 140 cm wide for a dress. How many meters of cloth will she need for the same 90 cm wide fabric dress? The result is rounded to whole meters. - Completely 83045
The diesel tank has a volume of 19.6 hl. The inflow oven, which flows 17.5 l per minute, was opened for 1.5 hours. How long does the inlet pipe need to be opened for the tank to be completely filled? - Warehouse 83041
At half past six in the evening, a truck left the warehouse at an average speed of 40 km/h. In 1.5 hours, a car drove behind him with an average speed of 70 km/h. How long and at what distance will the truck catch up from the warehouse?
Do you have unsolved problem that you need help? Ask a question, and we will try to solve it. Solving math problems.
