Reason - practice for 12 year olds
Number of problems found: 571
- A man 11
 A man is x years old. In 10 years, he will be twice as old as he was 5 years ago. How old will he be in 10 years?
A man is x years old. In 10 years, he will be twice as old as he was 5 years ago. How old will he be in 10 years? - Same remainder
 Find the greatest number that will divide 43, 91, and 183 so as to leave the same the remainder in each case.
Find the greatest number that will divide 43, 91, and 183 so as to leave the same the remainder in each case. - Calculate 83302
 Calculate the height of the rhombus ABCD on side BC if AB=7cm, BC=5.5cm, and the height of the first side on AB=4.4cm.
Calculate the height of the rhombus ABCD on side BC if AB=7cm, BC=5.5cm, and the height of the first side on AB=4.4cm. - Condition 83228
 Three boys, Ivo, Vlado, and Alan, are reading the same book, with the condition that they will read the same number of pages every day during the entire reading until they finish the book. Ivo reads 18 pages from it every day, Vlado reads 24 pages, and Al
Three boys, Ivo, Vlado, and Alan, are reading the same book, with the condition that they will read the same number of pages every day during the entire reading until they finish the book. Ivo reads 18 pages from it every day, Vlado reads 24 pages, and Al
- Beatka 83184
 Anna had 3 times more than Beatka. Cilka had 2 euros more than Beátka. They had a total of 52 euros. How much did each have?
Anna had 3 times more than Beatka. Cilka had 2 euros more than Beátka. They had a total of 52 euros. How much did each have? - Successful 83167
 Eighth-grade test results: 8D =? 8B = 47 8A = 44 8E = 37 8C = 28 Class 8A achieved exactly the average result. How many points did the winning class 8D get? By what % is class 8B more successful than class 8C?
Eighth-grade test results: 8D =? 8B = 47 8A = 44 8E = 37 8C = 28 Class 8A achieved exactly the average result. How many points did the winning class 8D get? By what % is class 8B more successful than class 8C? - Solution 83099
 There are spiders and flies on the window. They have a total of 38 legs. How many spiders and flies are there if a spider has 8 legs and a fly has 6? Just give one solution.
There are spiders and flies on the window. They have a total of 38 legs. How many spiders and flies are there if a spider has 8 legs and a fly has 6? Just give one solution. - Arithmetic 83094
 There were 31 students in the class, and the arithmetic average weight was 43 kg. Calculate the average weight in the class if a student weighing 91 kg has been added to the class.
There were 31 students in the class, and the arithmetic average weight was 43 kg. Calculate the average weight in the class if a student weighing 91 kg has been added to the class. - Characters 82998
 Adam wrote the following sum with five secret adders: a + bb + ccc + dddd + eeeee. He revealed that the characters "a, b, c, d, e" represent the different digits 1, 2, 3, 4, and 5 and that the resulting sum is divisible by 11. Which is the smallest and wh
Adam wrote the following sum with five secret adders: a + bb + ccc + dddd + eeeee. He revealed that the characters "a, b, c, d, e" represent the different digits 1, 2, 3, 4, and 5 and that the resulting sum is divisible by 11. Which is the smallest and wh
- Marbles 82974
 The bag has 5 red, 7 white, 10 yellow, and 6 black balls. At least how many marbles must be drawn from the bag to ensure that there will be 3 yellow ones among the drawn balls?
The bag has 5 red, 7 white, 10 yellow, and 6 black balls. At least how many marbles must be drawn from the bag to ensure that there will be 3 yellow ones among the drawn balls? - Calculate 82878
 Calculate in degrees the size of the acute angle made by the hands of the clock at half past six.
Calculate in degrees the size of the acute angle made by the hands of the clock at half past six. - Determine 82852
 The fan club has 275 members. Some members went to the match by train. Determine how many members rode when they could fill the wagons with either 60 or 80 seats.
The fan club has 275 members. Some members went to the match by train. Determine how many members rode when they could fill the wagons with either 60 or 80 seats. - Centimeters 82756
 Let us have a cube whose edge length is expressed in centimeters and is a natural number. What is the smallest number of such identical cubes that can be made into a cuboid with dimensions of 24 cm, 32 cm, and 60 cm? How long will the edge of these cubes
Let us have a cube whose edge length is expressed in centimeters and is a natural number. What is the smallest number of such identical cubes that can be made into a cuboid with dimensions of 24 cm, 32 cm, and 60 cm? How long will the edge of these cubes - Strawberries 82738
 Three classmates worked part-time during the summer vacation harvesting strawberries. Jan collected 145 baskets of strawberries during the entire time of the brigade. Peter collected 185 baskets. How many baskets did their classmate Stan collect, if we kn
Three classmates worked part-time during the summer vacation harvesting strawberries. Jan collected 145 baskets of strawberries during the entire time of the brigade. Peter collected 185 baskets. How many baskets did their classmate Stan collect, if we kn
- Performance_ 82318
 The dance troupe has 24 members. How many equal-sized groups of dancers can he divide into during a performance_
The dance troupe has 24 members. How many equal-sized groups of dancers can he divide into during a performance_ - Multiplied 82243
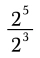 Zuzka divided 52 by 2 8 times and multiplied by 2 6 times. What number did she get?
Zuzka divided 52 by 2 8 times and multiplied by 2 6 times. What number did she get? - Supply 82149
 The water supply is enough for 12 horses for 16 days. How many horses will this supply of water last for 12 days?
The water supply is enough for 12 horses for 16 days. How many horses will this supply of water last for 12 days? - Machine 81767
 Four lathes machine 32 parts in 1 hour. How many parts does 1 turner machine have in 2 hours?
Four lathes machine 32 parts in 1 hour. How many parts does 1 turner machine have in 2 hours? - Classroom 81621
 On a classroom clock, the large (minute) hand on the clock will travel through an angle of 120 degrees in some time. What angle does the small (hour) hand pass in this time?
On a classroom clock, the large (minute) hand on the clock will travel through an angle of 120 degrees in some time. What angle does the small (hour) hand pass in this time?
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
