Isolating a variable in the formula - math word problems - page 31 of 145
Number of problems found: 2888
- Calculate 72624
 The perimeter of the ABC triangle is 19.6 cm. The following applies to the lengths of its sides: a: c = 1:2, b: c = 5:6. Calculate the lengths of all sides of the triangle ABC.
The perimeter of the ABC triangle is 19.6 cm. The following applies to the lengths of its sides: a: c = 1:2, b: c = 5:6. Calculate the lengths of all sides of the triangle ABC. - Arithmetic 72544
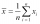 The arithmetic mean of two numbers is 12. The first number is 5. What is the value of the second number?
The arithmetic mean of two numbers is 12. The first number is 5. What is the value of the second number? - Dimensions of a prism
 Calculate the edge c and the surface S of a block if its volume is equal to 42 cubic centimeters, a = 6cm, b = 3.5cm, c =?
Calculate the edge c and the surface S of a block if its volume is equal to 42 cubic centimeters, a = 6cm, b = 3.5cm, c =? - Hypotenuse 72524
 We know the height of the hypotenuse h = 4cm and the hypotenuse c = 19cm in a right triangle. How to calculate the segments of legs - sections on the hypotenuse c1, c2
We know the height of the hypotenuse h = 4cm and the hypotenuse c = 19cm in a right triangle. How to calculate the segments of legs - sections on the hypotenuse c1, c2 - Trapezoid 45
 Trapezoid with: Area: 345 1/2 sq cm First base = 15 1/3 cm height= 4 1/5 cm What size is the second base?
Trapezoid with: Area: 345 1/2 sq cm First base = 15 1/3 cm height= 4 1/5 cm What size is the second base? - Circumference 72414
 Calculate the diagonal and the area of a square if its circumference is 10 centimeters.
Calculate the diagonal and the area of a square if its circumference is 10 centimeters. - Surface 72394
 The volume of the cube is 15625 cubic meters. Find the length of the edge and the surface of the cube.
The volume of the cube is 15625 cubic meters. Find the length of the edge and the surface of the cube. - Evaluate 25
 Evaluate the following expression: [ 3 + ( 40 ÷ 5 ) x ( 2 x 2 ) ] – 5 =
Evaluate the following expression: [ 3 + ( 40 ÷ 5 ) x ( 2 x 2 ) ] – 5 = - Length and width
 Use the 5-step procedure. The perimeter of a rectangle is 34 in. The length is 4 in less than three times the width. Find the length and width.
Use the 5-step procedure. The perimeter of a rectangle is 34 in. The length is 4 in less than three times the width. Find the length and width. - A hiker
 A hiker plans to hike up one side of a mountain and down the other side of points a mountain, each side of the mountain formed by a straight line. The angle of elevation at the starting point is 42.4 degrees, and the angle of elevation at the end is 48.3
A hiker plans to hike up one side of a mountain and down the other side of points a mountain, each side of the mountain formed by a straight line. The angle of elevation at the starting point is 42.4 degrees, and the angle of elevation at the end is 48.3 - A rectangle 10
 A rectangle has a length of 8 millimeters and an area of 216 square millimeters. What is the width? What is the perimeter?
A rectangle has a length of 8 millimeters and an area of 216 square millimeters. What is the width? What is the perimeter? - 150 percent
 One hundred fifty percent of what number is 15? 150% of x is 15.
One hundred fifty percent of what number is 15? 150% of x is 15. - Centimeters 72134
 The area of the square is equal to 1024 square centimeters. Calculate the perimeter of the square and the length of the side a.
The area of the square is equal to 1024 square centimeters. Calculate the perimeter of the square and the length of the side a. - Relatively 71994
 The two numbers are in a relatively 3:7 ratio. If the value of the larger number is 21, find a smaller number.
The two numbers are in a relatively 3:7 ratio. If the value of the larger number is 21, find a smaller number. - Observatory and aircraft
 The aircraft flying towards the observatory was aimed at a distance of 5300 m at an elevation angle of 28º and after 9 seconds at a distance of 2400 m at an elevation angle of 50º. Calculate the distance the plane has flown in this time interval, its spee
The aircraft flying towards the observatory was aimed at a distance of 5300 m at an elevation angle of 28º and after 9 seconds at a distance of 2400 m at an elevation angle of 50º. Calculate the distance the plane has flown in this time interval, its spee - The circumference 3
 The circumference of a cylindrical water tank is 62.8m. When it is 4/5 full of water, it holds 125.6 hectoliters. Find the depth of the tank.
The circumference of a cylindrical water tank is 62.8m. When it is 4/5 full of water, it holds 125.6 hectoliters. Find the depth of the tank. - Cylindrical tank
 The cylinder-shaped tank with a diameter of 100 cm is 50% full and contains 7850 l of water. What is the height of the tank?
The cylinder-shaped tank with a diameter of 100 cm is 50% full and contains 7850 l of water. What is the height of the tank? - An equivalent
 An equilateral triangle has the same perimeter as a rectangle whose sides are b and h (b > h). Considering that the area of the triangle is three times the area of the rectangle. What is the value of b/h?
An equilateral triangle has the same perimeter as a rectangle whose sides are b and h (b > h). Considering that the area of the triangle is three times the area of the rectangle. What is the value of b/h? - At 5:00
 At 5:00 AM, the room temperature was 20°C. After six hours, the reading was 28°C. The temperature rose to how many degrees? What was the average change in temperature per hour?
At 5:00 AM, the room temperature was 20°C. After six hours, the reading was 28°C. The temperature rose to how many degrees? What was the average change in temperature per hour? - Raymond
 Raymond is designing a 1-liter Tetrapak for milk. He knows that the rectangular base must be 50mm by 100mm. Therefore, he needs to make the height of the Tetrapak.
Raymond is designing a 1-liter Tetrapak for milk. He knows that the rectangular base must be 50mm by 100mm. Therefore, he needs to make the height of the Tetrapak.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
