Maths practice for 14 year olds - page 40 of 370

Number of problems found: 7388

Infinite speed
A runner runs her first lap of the track at an average speed of 5 km/h. How fast must she run her second lap so that her total average speed is 10 km/h?
Calculate 5
Calculate the area and perimeter of a trapezoid if side a=10, angle alpha 40 degrees, beta 50 degrees, and side c=3.
Compound fractions
Solve the compound fraction, use the known formulas, and shorten the: (4a²-12a+9)/(4a-6)
Construction 83662
Using Euclid's theorems, construct a triangle ABC with height on side c and size v = √8 cm. Choose the length of the hypotenuse c correctly. Write the construction procedure.
Hydraulic lift
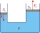Martin needs to lift a 1.5-ton car using a hydraulic device with pistons of sizes 2 cm² and 15 dm². How much force must the device exert on the small piston?
Circumference 83645
The area of a right triangle is 240 cm². Determine its circumference if the given lengths are suspended in a ratio of 5:12.
Groundwater
The groundwater for collecting rainwater has the shape of a prism with trapezoidal bases a=5 m, c=7 m, 4 meters apart. The depth of the tank is 3 meters. How many hectoliters of water can it hold at most if 8% of its volume is taken up by the pump and pip
3 weights
A two-arm lever has a 0.5 kg weight on the left arm at a distance of 64 cm from the axis of rotation and a 0.8 kg weight at a distance of 30 cm from the axis of rotation. How far on the right arm must the 0.7 kg weight be placed for the lever to be in bal
Tightened 83632
The key works like a lever, where one arm is the radius of the bolt, and the other is the length of the key. If key no. 12 (for screws with a diameter of 12 mm) and a length of 12 cm can be tightened with a maximum force of 100 N, what force does the wren
Heptagon perimeter
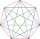Calculate a regular heptagon's perimeter if its shortest diagonal length is u=14.5cm.
Staircase - escalator
A moving staircase moves downwards at a speed of 0.6 m/s. The staircase makes an angle of 45° with the horizontal. A person weighing 80 kg walks upwards at a speed of 0.9 m/s. Determine the distance covered by the person and the work done by him before he
The Celebration
Five boys and five girls were nominated for a celebration at a local school. How many ways can the prom king, prom queen, and two other students be chosen from those nominated? (The king must be a boy, and the queen must be a girl)
Textbook 83602
A textbook with a workbook costs 14 euros. The workbook is 6 euros cheaper than the textbook. How much is the textbook, and how much is the workbook?
Harvest 83600
Martin brought twice as much harvest as Tomáš and Filip, 15 kg more than Martin. They got a total of 65 kg of harvest. How much did each person bring?
A lottery
In a lottery, a person chooses four different natural numbers at random from 1 to 10, and if these four numbers match the four numbers already fixed by the lottery committee, he wins the prize. What is the probability of winning the prize in the game? (Th
Representing 83587
Juraj paid 87 euros for ski training, representing 60% of the total. How much does ski training cost?
Different balls
We have four different boxes and three identical balls. Place the marbles in these boxes so that the boxes can contain one, two, three or none. How many other locations are there?
Cauliflower: 83523
Miss Kapustová sold vegetables in the market. Yesterday, she offered two types of cauliflower: a large one for 25 CZK and a small one for 15 CZK. She sold 8 crates of 20 heads and earned a total of CZK 3,270. How many large and how many small cauliflowers
Rectangular roof
Our house's roof is rectangular. When it rains, the water drains through the gutter. How much water flowed from our roof during a storm when we know that 12 liters of water fell on every 1 m² of surface? The roof width is 6m, the length is 9m, and the slo
Isosceles weight
A designer weight is made from a glass cube by cutting a three-sided prism with an isosceles triangle base that is right-angled and whose arm is half the length of the cube edge. What percentage of the cube is cut off when making the weight?

Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.