Reason - practice problems - page 4 of 108

Number of problems found: 2149

Into the bottle
The bottle can hold water weighing no more than 1 kg. Can you pour gasoline weighing the same amount into this bottle?
Three dice 2
What is the probability that two odd numbers will be the same when three dice are rolled?
Matej 2
Matej, Marko, Milan, and Matúš had a total of 205 football player cards with signatures. Marko has four times more than Matej. Matúš had two times less than Marko. Milan had 20 cards less than Matúš. How many cards did each have?
In the domestic
In the domestic express train, there are 1st and 2nd class carriages. There are 2x more 2nd class carriages than 1st class. There are 10 compartments in each carriage. In 1st class, each compartment has 6 seats, and in 2nd class carriages, there are eight
How many 172
How many five-digit numbers are there that have exactly 2 fours and exactly 3 sevens in their notation?
Bathroom 3
The bathroom measures 300x210 cm. What are the largest square tiles and how many will I need to cover the floor?
Relay
The relay race will be run for the class of Katka, Alice, Michaela, and Erika. Determine how many different orders there are in which the girls can run, as long as each of them can run in any position.
Competitor 2
In the race, 1 twelfth of the competitors finished ahead of me and 7 eighths of the competitors finished behind me. How many of us ran?
Ice rink
A rectangular rink measuring 15m and 20m long needs to be covered with a layer of ice 4.5cm high. How many liters of water are needed to create ice?
Rhombus 48
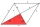A rhombus consists of four identical rhombuses with an area of 42 m². The angle alpha of each rhombus is 60°. What is its perimeter?
Equation - integers
Solve the equation with the unknown x from the field of natural numbers 1+6+11+16+. ... +x=970
How much 17
How many euros more will Mrs. Eva have if she increases her savings of €2,400 in the ratio 7 : 5?
Sweets
There are 12 sandwiches on a plate, 5 of which are poppy seeds and 7 are jam. How many cheese sandwiches must be added to them so that the probability that a randomly selected sandwich is poppy seed is 20%?
Rows of chairs
There are 15 chairs in the first row. There are 3 more chairs in each row. How many chairs are there in the first 20 rows?
Penny and rolls
For a hundred crowns I have to buy a hundred pieces of pastry at the prices of rolls of 0.50 crowns, bread 10 crowns, and a roll of 3 crowns. How much of what should I buy? (The Slovak koruna was the currency in Slovakia before the euro or the Czech korun
Seventh and multiplication table
If we add one-seventh of an unknown number to one-sixth of it, we get the sum 13. What is that number? 3rd grade, multiplication table
In a football
In a football tournament of eight teams, where each team played each other exactly once, points were awarded as follows: the winner of the match received 3 points, the loser received 0 points, and in the event of a draw, each team received 1 point. At the
Hip-roof
The roof consists of two isosceles trapezoids and two isosceles triangles. The roof plan is a rectangle with dimensions of 8m and 14m, and the roof ridge is 8m long. The height of the trapezoid is 5m, the height of the triangles is 4.2m. How many tiles ar
Stock inventory
At the beginning of each week, the stock inventory in the warehouse increases by 5% of the current level. At the end of every second week, 8% of the goods are issued from the warehouse. By how much percent will the stock in the warehouse be greater after
Elementary Art School
The music and art department in the elementary art school is attended by 86 students. The music department is attended by 45 students, the art department is attended by 53 students. Several students attend both departments. How many students attend the mu

Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.