Surface Area Calculation Problems for Solid Shapes. - page 22 of 52
Number of problems found: 1029
- Right-angled 4951
 Calculate the volume and surface area of the body that is created by cutting out a three-sided prism of the same height from a cuboid with dimensions of 10 cm, 15 cm, and 20 cm, whose base is a right-angled triangle with dimensions of 3 cm, 4 cm, and 5
Calculate the volume and surface area of the body that is created by cutting out a three-sided prism of the same height from a cuboid with dimensions of 10 cm, 15 cm, and 20 cm, whose base is a right-angled triangle with dimensions of 3 cm, 4 cm, and 5 - Calculate 4842
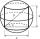 The area of the rotating cylinder shell is half the area of its surface. Calculate the surface of the cylinder if you know that the diagonal of the axial section is 5 cm.
The area of the rotating cylinder shell is half the area of its surface. Calculate the surface of the cylinder if you know that the diagonal of the axial section is 5 cm. - Cross-section of iron bar
 What is the mass of an iron bar 1.5 m long, the cross-section of which is a rhombus with side a = 45 mm and a corresponding height of 40 mm? Iron density ρ = 7.8 g/cm³? What is the surface of the iron rod?
What is the mass of an iron bar 1.5 m long, the cross-section of which is a rhombus with side a = 45 mm and a corresponding height of 40 mm? Iron density ρ = 7.8 g/cm³? What is the surface of the iron rod? - Block-shaped 31741
 We will paint the block-shaped pool, with the dimensions of the bottom a = 25 m and b = 15 m and the height c = 3.5 m. If one kg is enough for five square meters of paint, how many kg of paint will we need?
We will paint the block-shaped pool, with the dimensions of the bottom a = 25 m and b = 15 m and the height c = 3.5 m. If one kg is enough for five square meters of paint, how many kg of paint will we need? - Quadrilateral prism
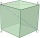 Calculate the volume and surface area of a regular quadrilateral prism with base edge a=24 cm if the body diagonal makes an angle of 66° with the base.
Calculate the volume and surface area of a regular quadrilateral prism with base edge a=24 cm if the body diagonal makes an angle of 66° with the base. - An Elizabethan collar
 An Elizabethan collar is used to prevent an animal from irritating a wound. The angle between the opening (diameter 6 inches) with a 16-inch diameter and the side of the collar is 53 degrees. Find the surface area of the collar shown.
An Elizabethan collar is used to prevent an animal from irritating a wound. The angle between the opening (diameter 6 inches) with a 16-inch diameter and the side of the collar is 53 degrees. Find the surface area of the collar shown. - The roof
 The house's roof has the shape of a regular quadrilateral pyramid 5 m high and the edge of the base 7 m. How many tiles with an area of 540 cm² are needed?
The house's roof has the shape of a regular quadrilateral pyramid 5 m high and the edge of the base 7 m. How many tiles with an area of 540 cm² are needed? - Truncated pyramid
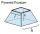 The concrete pedestal in a regular quadrilateral truncated pyramid has a height of 12 cm; the pedestal edges have lengths of 2.4 and 1.6 dm. Calculate the surface of the base.
The concrete pedestal in a regular quadrilateral truncated pyramid has a height of 12 cm; the pedestal edges have lengths of 2.4 and 1.6 dm. Calculate the surface of the base. - Cuboid - box
 The box has the shape of a cuboid with dimensions of 5 cm and 30 mm. Calculate the box's height if the cuboid's volume is 0.60 dm³. Calculate the surface area of the box. (calculation of height from the volume, calculation of area from the formula, keep
The box has the shape of a cuboid with dimensions of 5 cm and 30 mm. Calculate the box's height if the cuboid's volume is 0.60 dm³. Calculate the surface area of the box. (calculation of height from the volume, calculation of area from the formula, keep - Storm and roof
 The roof of the building is a cone with a height of 3 meters and a radius equal to half the height of the roof. How many m² of the roof need to be repaired if 20% were damaged in a storm?
The roof of the building is a cone with a height of 3 meters and a radius equal to half the height of the roof. How many m² of the roof need to be repaired if 20% were damaged in a storm? - Calculate the pool
 Calculate how many square meters are needed to line the pool 6 meters long, 4 meters wide, and 1.5 meters deep. Add 10% to waste.
Calculate how many square meters are needed to line the pool 6 meters long, 4 meters wide, and 1.5 meters deep. Add 10% to waste. - Angle of deviation
 The surface of the rotating cone is 30 cm² (with a circle base), and its surface area is 20 cm². Calculate the deviation of this cone's side from the base's plane.
The surface of the rotating cone is 30 cm² (with a circle base), and its surface area is 20 cm². Calculate the deviation of this cone's side from the base's plane. - Cubes
 Carol with cut bar 12 cm x 12 cm x 135 cm to the cubes. Find the sum of all the surfaces of the resulting cubes.
Carol with cut bar 12 cm x 12 cm x 135 cm to the cubes. Find the sum of all the surfaces of the resulting cubes. - Church roof
 The roof of the church tower has the shape of a regular tetrahedral pyramid with a base edge length of 5.4 meters and a height of 5 m. It was found that the 27% covering of the roof area needs to be corrected. What amount of material will be required?
The roof of the church tower has the shape of a regular tetrahedral pyramid with a base edge length of 5.4 meters and a height of 5 m. It was found that the 27% covering of the roof area needs to be corrected. What amount of material will be required? - Triangular pyramid
 Calculate the volume and surface area of a regular triangular pyramid with a height equal to the base edge, which is 10 cm long.
Calculate the volume and surface area of a regular triangular pyramid with a height equal to the base edge, which is 10 cm long. - Oceans
 The Earth's surface is approximately 510,000,000 km² and is 7/10 covered by oceans. Of which 1/2 covers the Pacific Ocean, the Atlantic Ocean 1/4, the Indian Ocean 1/5, and the Arctic Ocean 1/20. What parts of the Earth's surface cover each ocean?
The Earth's surface is approximately 510,000,000 km² and is 7/10 covered by oceans. Of which 1/2 covers the Pacific Ocean, the Atlantic Ocean 1/4, the Indian Ocean 1/5, and the Arctic Ocean 1/20. What parts of the Earth's surface cover each ocean? - Bathroom
 How much CZK do we pay for lining the perimeter walls of the bathroom with rectangular shapes with dimensions of 3.5 m and 4 m, high 1.5 m if 1 square m tile costs 300 CZK?
How much CZK do we pay for lining the perimeter walls of the bathroom with rectangular shapes with dimensions of 3.5 m and 4 m, high 1.5 m if 1 square m tile costs 300 CZK? - 4side pyramid
 Calculate the volume and surface of the regular four-sided pyramid whose base edge is 4 cm long. The angle from the plane of the sidewall and base plane is 60 degrees.
Calculate the volume and surface of the regular four-sided pyramid whose base edge is 4 cm long. The angle from the plane of the sidewall and base plane is 60 degrees. - The cone
 The cone's lateral surface area is 4 cm², and the area of the base is 2 cm². Find the angle in degrees (deviation) of the cone sine and the cone base plane. (The cone side is the segment joining the vertex cone with any point of the base circle. All sides
The cone's lateral surface area is 4 cm², and the area of the base is 2 cm². Find the angle in degrees (deviation) of the cone sine and the cone base plane. (The cone side is the segment joining the vertex cone with any point of the base circle. All sides - Colour - billboard
 Shelftalker has the shape of a parallelogram. Its length is 4.9 m, and its corresponding height is 3.5 meters. Calculate how much (kg) paint must be purchased for redecoration if 1 kg covers 4 m² of shelf talker surface.
Shelftalker has the shape of a parallelogram. Its length is 4.9 m, and its corresponding height is 3.5 meters. Calculate how much (kg) paint must be purchased for redecoration if 1 kg covers 4 m² of shelf talker surface.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
