Surface Area Calculation Problems for Solid Shapes. - page 6 of 52
Number of problems found: 1027
- Determine 7488
The lengths of the edges of the two cubes are in the ratio 2:3. Determine how many times the surface of the larger cube is larger than the surface of the smaller cube. - Thirtieth 5806
The surface of the pond is covered with water lilies so that the area covered by water lilies doubles per day. On the thirtieth day, the surface was full of water lilies. On how many days was half of the pond covered with water lilies? - The surface
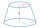The surface of a truncated rotating cone with side s = 13 cm is S = 510π cm². Find the radii of the bases when their difference in lengths is 10cm. - Surface and volume
Find the surface and volume of a cuboid whose dimensions are 1 m, 50 cm, and 6 dm. - Cube surface and volume
The surface of the cube is 500 cm². How much cm³ will its volume be? - Calculate 62864
The block volume is 1440 cm3, its surface is 792 cm2, and the area of one of its walls is 92 cm². Calculate the lengths of its sides. - Identical 36423
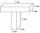We glued the letter T from two identical wooden blocks, 5 cm x 5 cm x 10 cm, and wanted to paint it. How big will it be? - Cylinder 11141
The area of the cylinder shell is 300 cm², the height of which is equal to the diameter of the base. Find the surface of the cylinder. - Calculate 5624
The cube has a surface area of 110.6 cm². Calculate the length of its edge. - Cuboid - ratio
Find the volume of a block whose dimensions are in the ratio 2:3:4 and the surface is 117 dm². - Cylindrical container
An open-topped cylindrical container has a volume of V = 3140 cm³. Find the cylinder dimensions (radius of base r, height v) so that the least material is needed to form the container. - Sheet of paper
Is the sheet of paper measuring 18 and 25 cm enough for taping 9 cm cubes with an edge? (1 = yes, 0 = no) - Cuboid
The volume of the cuboid is 245 cm³. Each cuboid edge length can be expressed by an integer greater than 1 cm. What is the surface area of the cuboid? - The block The block, the edges formed by three consecutive GP members, has a surface area of 112 cm². The sum of the edges that pass through one vertex is 14 cm. Calculate the volume of this block.
- Equilateral cylinder
A sphere is inserted into the rotating equilateral cylinder (touching the bases and the shell). Prove that the cylinder has both a volume and a surface half larger than an inscribed sphere. - Volume 62064
The open box has the shape of a cube. We used 80 dm² of paper to glue on it. What is the volume of this box? - Rotary cylinder
In the rotary cylinder, it is given: surface S = 96 cm² and volume V = 192 cm cubic. Calculate its radius and height. - Calculate 19083
A) The wooden cube has an edge 14.7 cm long. Calculate its surface area and volume. B) The metal cube's inner edge is 13.6 cm long. How many cm of water can fit in it? - Two cubes
The surfaces of two cubes, one of which has an edge of 22 cm longer than the second, differ by 19272 cm². Calculate the edge length of both cubes. - Three cubes
The body was created by gluing three identical cubes. Its volume is 192 cm³. What is its surface in dm²?
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
