Surface Area Calculation Problems for Solid Shapes. - page 23 of 52
Number of problems found: 1029
- Pyramid a+h
 Calculate the pyramid's volume and surface area with the edge and height a = 26 cm. h = 3 dm.
Calculate the pyramid's volume and surface area with the edge and height a = 26 cm. h = 3 dm. - The cap
 A rotating cone shapes a jester hat. Calculate how much paper is needed for the cap 53 cm high when the head circumference is 45 cm.
A rotating cone shapes a jester hat. Calculate how much paper is needed for the cap 53 cm high when the head circumference is 45 cm. - School model
 The beech school model of a regular quadrilateral pyramid has a base 20 cm long and 24 cm high. Calculate a) the surface of the pyramid in square decimeters, b) the mass of the pyramid in kilograms if the density of the beech is ρ = 0,8 g/cm³
The beech school model of a regular quadrilateral pyramid has a base 20 cm long and 24 cm high. Calculate a) the surface of the pyramid in square decimeters, b) the mass of the pyramid in kilograms if the density of the beech is ρ = 0,8 g/cm³ - Quadrilateral 46431
 Calculate the volume V and the surface S of a regular quadrilateral pyramid, the base edge and height of which are the same size as the edge of a cube with a volume V1 = 27m3
Calculate the volume V and the surface S of a regular quadrilateral pyramid, the base edge and height of which are the same size as the edge of a cube with a volume V1 = 27m3 - Quadrilateral 43941
 Calculate the surface of a 3.5 m high quadrilateral pyramid with a rectangular base with dimensions of 3 m and 1.8 m.
Calculate the surface of a 3.5 m high quadrilateral pyramid with a rectangular base with dimensions of 3 m and 1.8 m. - Cylindrical 28331
 How many crowns will the paint cost to paint a cylindrical container (d = 4.2 m, h = 5.5 m) when about 5 m² of paint is painted from 1 kg of color, and 1 kg of paint costs 115 CZK?
How many crowns will the paint cost to paint a cylindrical container (d = 4.2 m, h = 5.5 m) when about 5 m² of paint is painted from 1 kg of color, and 1 kg of paint costs 115 CZK? - Half-cylinder 9961
 The cattle water feeding trough is a half-cylinder with a length of 2 m and a width of 0.8 m. How many m³ of water can be poured into the gutter? How many m² do we need to produce 25 such gutters?
The cattle water feeding trough is a half-cylinder with a length of 2 m and a width of 0.8 m. How many m³ of water can be poured into the gutter? How many m² do we need to produce 25 such gutters? - Measuring 6357
 Determine the length of the edge of the cube, the surface of which is equal to 60% of the surface of a block measuring 7cm, 8cm, 6cm
Determine the length of the edge of the cube, the surface of which is equal to 60% of the surface of a block measuring 7cm, 8cm, 6cm - Perpendicular 5865
 We cut the cube with two mutually perpendicular cuts, each parallel to one of the cube's walls. By what percentage is the sum of the surfaces of all cuboids created in this way greater than the surface of the original cube?
We cut the cube with two mutually perpendicular cuts, each parallel to one of the cube's walls. By what percentage is the sum of the surfaces of all cuboids created in this way greater than the surface of the original cube? - Centimeters 65884
 The plastic bucket has the shape of a cylinder with a diameter of 25 cm and a height of 40 cm. How many square centimeters are needed to produce it? How many liters does it contain when filled 5 cm below the rim?
The plastic bucket has the shape of a cylinder with a diameter of 25 cm and a height of 40 cm. How many square centimeters are needed to produce it? How many liters does it contain when filled 5 cm below the rim? - Surface and volume
 Find the surface and volume of the rotating cone if the circumference of its base is 62.8 m and the side is 25 m long.
Find the surface and volume of the rotating cone if the circumference of its base is 62.8 m and the side is 25 m long. - Paint the walls
 It is necessary to paint the walls and ceiling of the warehouse, which is 10 m long, 4 m wide, and 3 m high. How many CZK (Czech crowns) will it cost to paint if it costs 200 CZK to paint 1 m²?
It is necessary to paint the walls and ceiling of the warehouse, which is 10 m long, 4 m wide, and 3 m high. How many CZK (Czech crowns) will it cost to paint if it costs 200 CZK to paint 1 m²? - Deviation - slope angle
 Calculate the volume and surface of the rotating cone if its height is 10 cm and the side has a deviation of 30° from the base plane.
Calculate the volume and surface of the rotating cone if its height is 10 cm and the side has a deviation of 30° from the base plane. - Ball screen
 The diameter of the ball screen is 30 cm. If we add 5% of the material to be sewn, how many m² of fabric do we need to make?
The diameter of the ball screen is 30 cm. If we add 5% of the material to be sewn, how many m² of fabric do we need to make? - Cone side
 Calculate the volume and area of the cone whose height is 10 cm, and the axial section of the cone has an angle of 30 degrees between height and the cone side.
Calculate the volume and area of the cone whose height is 10 cm, and the axial section of the cone has an angle of 30 degrees between height and the cone side. - A concrete pedestal
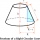 A concrete pedestal has the shape of a right circular cone and a height of 2.5 feet. The diameters of the upper and lower bases are 3 feet and 5 feet, respectively. Determine the pedestal's lateral surface area, total surface area, and volume.
A concrete pedestal has the shape of a right circular cone and a height of 2.5 feet. The diameters of the upper and lower bases are 3 feet and 5 feet, respectively. Determine the pedestal's lateral surface area, total surface area, and volume. - Calculate cylinder
 In the rotating cylinder, it is given: V = 120 cm3, v = 4 cm. Calculate r, S mantle.
In the rotating cylinder, it is given: V = 120 cm3, v = 4 cm. Calculate r, S mantle. - Roof 7
 The roof is a regular quadrangular pyramid with a base edge of 12 m, and a height of 4 m. How many percent is folds and waste if in construction was consumed 181.4m² of the plate was?
The roof is a regular quadrangular pyramid with a base edge of 12 m, and a height of 4 m. How many percent is folds and waste if in construction was consumed 181.4m² of the plate was? - Tetrahedral prism
 Calculate the area and volume of a tetrahedral prism that has a base rhomboid shape, and its dimensions are: a = 12 cm, b = 70 mm, v_a = 6 cm, v_h = 1 dm.
Calculate the area and volume of a tetrahedral prism that has a base rhomboid shape, and its dimensions are: a = 12 cm, b = 70 mm, v_a = 6 cm, v_h = 1 dm. - Rotary bodies
 The rotating cone and the rotary cylinder have the same volume of 180 cm³ and the same height, v = 15 cm. Which of these two bodies has a larger surface area?
The rotating cone and the rotary cylinder have the same volume of 180 cm³ and the same height, v = 15 cm. Which of these two bodies has a larger surface area?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
