Rotating cone
If the side of the rotating cone is 150 mm long and the circumference of the base is 43.96 cm, find its surface and volume.
Correct answer:
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
See also our right triangle calculator.
See also our right triangle calculator.
You need to know the following knowledge to solve this word math problem:
- algebra
- expression of a variable from the formula
- solid geometry
- cone
- surface area
- planimetrics
- Pythagorean theorem
- right triangle
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Surface and volume
Find the surface and volume of the rotating cone if the circumference of its base is 62.8 m and the side is 25 m long. - Circumference 3370
Calculate the surface and volume of the rotating cone, whose base circumference is 125.6 cm and the side is 25 cm long. - Circumference 15653 Calculate the surface and volume of a rotating cone whose base circumference is 125.6 cm and the side is 25 cm long.
- Circumference 27581
The rotating cone has a base circumference of 62.8 cm. And a height of 0.7 dm. Calculate its surface area and volume.
- Cone - side
If the cone's height is 125 mm and its side length is 17 cm, find its surface area and volume. - Surface area and volume Find the surface area and volume of a rotating cone whose diameter is 60 mm and side length is 3.4 cm.
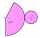- Circumference 27161 Sketch the cone mesh and add the side length, the arc length of the circle, and the circle length to it, if you know: the side length of the cone: s = 51.9 cm cone base circumference = O = 151 mm.
