Unit conversion - practice problems - page 5 of 132
Number of problems found: 2626
- One side 4
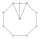 One side of a regular octagon is 12 inches. Find the apothem and its area.
One side of a regular octagon is 12 inches. Find the apothem and its area. - Three 235
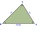 Three houses form a triangular shape. House A is 50 feet from house C and house B is 60 feet from house C. The measure is angle ABC is 45 degrees. Draw a picture and find the distance between A and B.
Three houses form a triangular shape. House A is 50 feet from house C and house B is 60 feet from house C. The measure is angle ABC is 45 degrees. Draw a picture and find the distance between A and B. - A boy 5
 A boy starts at A and walks 3km east to B. He then walks 4km north to C. Find the bearing of C from A.
A boy starts at A and walks 3km east to B. He then walks 4km north to C. Find the bearing of C from A. - Paper
 The drawing paper has dimensions 220mm and 308mm. Pupils should cut it into squares of the same size so that they are as large as possible. Determine the dimensions of the square in cm and the number of squares.
The drawing paper has dimensions 220mm and 308mm. Pupils should cut it into squares of the same size so that they are as large as possible. Determine the dimensions of the square in cm and the number of squares. - Konrad
 Konrad coaches football. He cycles 3 km to the stadium at an average 12 km/h speed. How long does Konrad take to cycle to the stadium?
Konrad coaches football. He cycles 3 km to the stadium at an average 12 km/h speed. How long does Konrad take to cycle to the stadium? - There 32
 There are 20 magazines in a pile. Each magazine is 5 mm thick. How high is the pile in meters?
There are 20 magazines in a pile. Each magazine is 5 mm thick. How high is the pile in meters? - FRAMES
 Joe is making picture frames out of wood. The length of each frame is 10 inches, and the width is 8 inches. Each piece of wood used to make the frames is 8 feet long. How many pieces of wood will he need to make 10 picture frames? Clue: find the perimeter
Joe is making picture frames out of wood. The length of each frame is 10 inches, and the width is 8 inches. Each piece of wood used to make the frames is 8 feet long. How many pieces of wood will he need to make 10 picture frames? Clue: find the perimeter - A rectangular 11
 A rectangular plot of land has sides that are 1200m long and 900m wide. If a hectare (10000m²) of the land costs R5200,00, the cost of the entire plot is:
A rectangular plot of land has sides that are 1200m long and 900m wide. If a hectare (10000m²) of the land costs R5200,00, the cost of the entire plot is: - David 5
 David was riding his bicycle at a speed of 26.5 kilometers per hour (km/h). Use the fact that 1 kilometer is approximately equal to 0.6214 miles to convert this speed to miles per hour (mile/h)
David was riding his bicycle at a speed of 26.5 kilometers per hour (km/h). Use the fact that 1 kilometer is approximately equal to 0.6214 miles to convert this speed to miles per hour (mile/h) - A soccer
 A soccer field (football pitch) has a length of 101.8 m and a width of 69.8 m. Find the total area of the field in square meters (m2) and convert this measurement to square yards (yd2). Use the fact that 1 yard = 0.9144 m. Round your answer to the nearest
A soccer field (football pitch) has a length of 101.8 m and a width of 69.8 m. Find the total area of the field in square meters (m2) and convert this measurement to square yards (yd2). Use the fact that 1 yard = 0.9144 m. Round your answer to the nearest - A radio antenna
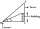 Avanti is trying to find the height of a radio antenna on the roof of a local building. She stands at a horizontal distance of 21 meters from the building. The angle of elevation from her eyes to the roof (point A) is 42°, and the angle of elevation from
Avanti is trying to find the height of a radio antenna on the roof of a local building. She stands at a horizontal distance of 21 meters from the building. The angle of elevation from her eyes to the roof (point A) is 42°, and the angle of elevation from - Piece of a wire
 A piece of wire is bent into the shape of a triangle. Two sides have lengths of 24 inches and 21 inches. The angle between these two sides is 55°. What is the length of the third side to the nearest hundredth of an inch? A: The length of the third side is
A piece of wire is bent into the shape of a triangle. Two sides have lengths of 24 inches and 21 inches. The angle between these two sides is 55°. What is the length of the third side to the nearest hundredth of an inch? A: The length of the third side is - Map scale
 On a map, on a scale of 1:50000, what is the distance in kilometers that 6 cm on the map represents?
On a map, on a scale of 1:50000, what is the distance in kilometers that 6 cm on the map represents? - Martha 3
 Martha placed 225 liters of water into a child swimming pool that holds 3.8 hectoliters. How much more water does Martha need to fill the pool?
Martha placed 225 liters of water into a child swimming pool that holds 3.8 hectoliters. How much more water does Martha need to fill the pool? - Subtract polar forms
 Solve the following 5.2∠58° - 1.6∠-40° and give answer in polar form
Solve the following 5.2∠58° - 1.6∠-40° and give answer in polar form - The factory 3
 The factory is 18 km away from the city. A cyclist leaves the factory for the city, and half an hour after him from the same place, a motorcyclist arrives 6 minutes before the cyclist in the city. Find the speed of each, knowing that the speed of the cycl
The factory is 18 km away from the city. A cyclist leaves the factory for the city, and half an hour after him from the same place, a motorcyclist arrives 6 minutes before the cyclist in the city. Find the speed of each, knowing that the speed of the cycl - Salt water
 The ratio of water (in liters) to salt (in grams) needs to be 3 to 2. If we add 10 grams of salt, how much water do we need to add?
The ratio of water (in liters) to salt (in grams) needs to be 3 to 2. If we add 10 grams of salt, how much water do we need to add? - Scale model
 In a model train set, 1.38 inches represents one foot in real life. The height of One World Trade Center in New York City is 1776 feet. How tall would a scale model of the building be? Should you calculate 1776 x 1.38 or 1776 ÷ 1.38?
In a model train set, 1.38 inches represents one foot in real life. The height of One World Trade Center in New York City is 1776 feet. How tall would a scale model of the building be? Should you calculate 1776 x 1.38 or 1776 ÷ 1.38? - The long
 The long side of a rectangular frame is 2′9″, and the short side is 1′3″. What is the area of the frame in square feet?
The long side of a rectangular frame is 2′9″, and the short side is 1′3″. What is the area of the frame in square feet? - Workers
 Suppose John starts work at 8:45 AM and finishes at 5:15 PM. He has 90 minutes of breaks. How many hours does he work in 5 days?
Suppose John starts work at 8:45 AM and finishes at 5:15 PM. He has 90 minutes of breaks. How many hours does he work in 5 days?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
