Third member
Determine the third member of the AP if a4=93, d=7.5.
Final Answer:

You need to know the following knowledge to solve this word math problem:
algebraGrade of the word problem
Related math problems and questions:
- AP - basics
 Determine the first member and differentiate the following sequence: a3-a5=24 a4-2a5=61
Determine the first member and differentiate the following sequence: a3-a5=24 a4-2a5=61 - Difference 3832
 Determine the difference AP if a1 = -7.5 and a1 + a2 = 4.8.
Determine the difference AP if a1 = -7.5 and a1 + a2 = 4.8. - Geometric seq
 Find the third member of geometric progression if a1 + a2 = 36 and a1 + a3 = 90. Calculate its quotient.
Find the third member of geometric progression if a1 + a2 = 36 and a1 + a3 = 90. Calculate its quotient. - Difference AP
 Calculate the difference of arithmetic progression if the sum of its first 10 members Sn = 1325 and the first member is a1 = 20
Calculate the difference of arithmetic progression if the sum of its first 10 members Sn = 1325 and the first member is a1 = 20 - Sequence 5535
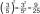 Find the value of the third member of the sequence if the sequence is given by: 3^n + 93.
Find the value of the third member of the sequence if the sequence is given by: 3^n + 93. - Determine 3904
 Determine the seventh GP member if a1 = -3.4, q = 5
Determine the seventh GP member if a1 = -3.4, q = 5 - Difference 3908
 Determine the fourth term and the difference AP if a1 = 3.2 and a2 + a3 = 7.
Determine the fourth term and the difference AP if a1 = 3.2 and a2 + a3 = 7.
