Numbers - practice problems
Mathematics is the science of numbers and counting. The original numbers that began to be counted were natural numbers - one, two, three, and so on. To write numbers, we use the digits 0,1,2,3,4,5,6,7,8,9. We use 10 digits in the decimal system.Number of problems found: 6093
- Equivalent fractions 3
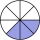 What fraction is equivalent to 1/3? Write three equivalent fractions to 1/3.
What fraction is equivalent to 1/3? Write three equivalent fractions to 1/3. - Mass fraction 2
 What fraction is 60kg of 150kg?
What fraction is 60kg of 150kg? - Complex number z
 Let z = -5 + i and w = 4 - 2i. Compute z - w and write your final answer in a + bi form. x = z - w
Let z = -5 + i and w = 4 - 2i. Compute z - w and write your final answer in a + bi form. x = z - w - Money fraction
 You have 8 euros and spend 5 euros. What fraction did you spend?
You have 8 euros and spend 5 euros. What fraction did you spend? - Amelia
 Amelia and Ray were making cupcakes. In a glass bowl, they added 3 cups of flour, 1 1/3 cups of vegetable oil, 1/2 cup of butter, 1/4 cup of chocolate chips, and 2 more cups of other ingredients. How many cups of batter are in the bowl?
Amelia and Ray were making cupcakes. In a glass bowl, they added 3 cups of flour, 1 1/3 cups of vegetable oil, 1/2 cup of butter, 1/4 cup of chocolate chips, and 2 more cups of other ingredients. How many cups of batter are in the bowl? - Negative number 2
 Haley is trying out a new racing game on her tablet. Her score decreases by 100 points when her driving car gets a flat tire. What integer represents the change in Haley's score when she gets a flat tire?
Haley is trying out a new racing game on her tablet. Her score decreases by 100 points when her driving car gets a flat tire. What integer represents the change in Haley's score when she gets a flat tire? - Clock ratio
 What is six hours to 10 hours?
What is six hours to 10 hours? - Improper to mixed number
 Convert improper fraction 34/7 to a mixed fraction.
Convert improper fraction 34/7 to a mixed fraction. - Oranges
 There are 50 oranges in a bag. If ten of these oranges are bad, what fraction of them are good?
There are 50 oranges in a bag. If ten of these oranges are bad, what fraction of them are good? - Puzzle game
 In a letter puzzle game, John can use every alphabet only once. He used only 8 alphabets to solve the puzzle. What fraction of the 26 alphabets did he use? Express your answer as a fraction in the simplest form.
In a letter puzzle game, John can use every alphabet only once. He used only 8 alphabets to solve the puzzle. What fraction of the 26 alphabets did he use? Express your answer as a fraction in the simplest form. - Change 8
 Change this mixed number into an improper fraction of 2 1/9
Change this mixed number into an improper fraction of 2 1/9 - Lilliana
 Lilliana wrote a number. She gave the following clues to her number: The digit in the tenths place is 4 The digit in the one's place is 8 The digit in the thousands place is 9 The digit in the hundreds place is 2 Find Lilliana's number.
Lilliana wrote a number. She gave the following clues to her number: The digit in the tenths place is 4 The digit in the one's place is 8 The digit in the thousands place is 9 The digit in the hundreds place is 2 Find Lilliana's number. - A scuba
 A scuba diver swims to a depth of 12 15/16 meters below sea level. Which of the following shows the decimal representation of -12 15/16? Write as decimal value...
A scuba diver swims to a depth of 12 15/16 meters below sea level. Which of the following shows the decimal representation of -12 15/16? Write as decimal value... - Decimal place
 What is the digit's place value to the right of 3 in 2.438?
What is the digit's place value to the right of 3 in 2.438? - Reduce fractions
 The following fraction is reduced to its lowest terms except one. Which of these: A. 98/99 B. 73/179 C. 1/250 D. 81/729
The following fraction is reduced to its lowest terms except one. Which of these: A. 98/99 B. 73/179 C. 1/250 D. 81/729 - A water
 A water jug has 1 5/8 liters of liquid. How do you write this mixed number as a decimal?
A water jug has 1 5/8 liters of liquid. How do you write this mixed number as a decimal? - Write as decimals
 Write two hundred four thousandths in decimal form.
Write two hundred four thousandths in decimal form. - Out 550,000.00
 Out of 550,000.00, an amount of 325,000.00 was used. What fraction of the total amount was used?
Out of 550,000.00, an amount of 325,000.00 was used. What fraction of the total amount was used? - One-fifth
 What is 1/5 as a decimal? Round your answer to three decimal places.
What is 1/5 as a decimal? Round your answer to three decimal places. - Half-hour
 How many minutes are in 1/2h (in a half hour)?
How many minutes are in 1/2h (in a half hour)?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
