Numbers - math word problems - page 306 of 307
Number of problems found: 6121
- Cis notation
Evaluate the multiplication of two complex numbers in cis notation: (6 cis 120°)(4 cis 30°) Write the result in cis and Re-Im notation. - Octahedron - sum
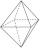On each wall of a regular octahedron is written one of the numbers 1, 2, 3, 4, 5, 6, 7, and 8, wherein on different sides are different numbers. John makes the sum of the numbers written on three adjacent walls for each wall. Thus got eight sums, which al - Fifth 3871
What is the sum of the fifth root of 243? - Goniometric form
Determine the goniometric form of a complex number z = √ 110 +4 i. - Three-digit number
Find all three-digit numbers n with three different non-zero digits divisible by the sum of all three two-digit numbers we get when we delete one digit in the original number. - Determine 80714
Three different numbers are given. The average of the average of two smaller numbers and the average of the two larger numbers is equal to the average of all three numbers. The average of the smallest and largest number is 2022. Determine the sum of the t - Third roots
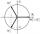Determine the sum of the three complex third roots of the number 64 .
- Determine 3882
Determine the sum of the three square roots of 343. - The number - digits
The vortex of the three given digits formed different three-digit numbers. When she added up all these numbers, she published 1554. What numbers did Vierka use? - Modulus and argument Find the mod z and argument z if z=i
- Apartment 71114
A father and son paint the apartment together in 6 hours. My father would paint the apartment in 9 hours. In how many hours would the son paint the apartment himself? - Dice - 5 times
We roll the dice five times. Make sentences: a) 3 events that definitely cannot happen. Write a reason for each. b) 3 events that will definitely occur; write a reason for each. Another problem: 3 events that may or may not occur for each. Write a reason. - Complex roots Find the sum of the fourth square root of the number 16.
- Calculate roots of z
Calculate the ratio of the two fifth roots of the number 32. - Triangle in circle
The vertices of the triangle ABC lie on a circle with a radius 3, which is divided into three parts in the ratio 4:4:4. Calculate the circumference of the triangle ABC.
- Observer
The observer sees a straight fence 100 m long in 30° view angle. From one end of the fence is 119 m. How far is it from the other end of the fence? - Gon functions
Decide which numbers (values of trigonometric functions) are positive or negative (or zero). Positive mark +1 and negative -1. - Slope
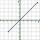What is the slope of a line with an inclination -325°? - Instantaneous 76754
For a dipole, calculate the complex apparent power S and the instantaneous value of the current i(t), given: R=10 Ω, C=100uF, f=50 Hz, u(t)= square root of 2, sin( ωt - 30 °). Thanks for any help or advice. - Cuboid
Find the dimensions of cuboids a, b, and c; if diagonal d=9 dm has an angle with edge α=55° and has an angle with edge b β=58°
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
