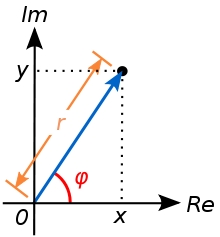
Modulus and argument
Find the mod z and argument z if z=i
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
arithmeticplanimetricsnumbersgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Modulo
Find x in the modulo equation: 47x = 4 (mod 9) Hint - read as what number 47x divided by 9 (modulo 9) gives remainder 4. - Simple coefficient
Find the value of k; if x = 3, y = 2 is a solution of the equation 2x + 3y = k. - Find x
Solve: if 2(x-1)=14, then x= (solve an equation with one unknown) - Angles - triangle
Find the measure of the angles of the triangle ABC if: the measure of angle A is the measure of angle C and the measure of angle B =½ of the measure of angle C.
- Complex equation
If c - d = 2 and c = 12 + 7 i, find d. Write the result in the form of a + bi. - Sets
If X = {1, 2, 3, 4, 5 . . .10}, Y = {2, 4, 6,. . . 20} and Z = {x: x is an integer, 15 ≤ x ≤ 25 }. Find (a) X ∩ Y, (b) X ∩ Z, (c) n(X ∪ Y), and (d) n(X ∪ Z) - Expressions
Find out value of expressions if a = -1, b =2: x=b - 2a - ab y=a³ - b² - 2ab z=a² b³ - a³ b² w=a + b + a³ - b²
