Math practice for 13 year olds - page 92 of 422
Number of problems found: 8425
- Perimeter+mixed
Find the perimeter of a triangle whose sides are 5 1/2 cm, 7 3/5 cm, and 3 1/4 cm, respectively. - Senior students
There are 7000 students at mountain high school, and 2/7 of these students are seniors. If 2/5 of the seniors favor the school forming a debate team and 3/8 of the remaining students, not seniors, are also forming a debate team, how many students do not f - Žaneta 78044 Juraj and Žaneta are 48 years old. Juraj is twice as old as Žaneta. How old is Juraj, and how old is Žaneta?
- Photographs 78034
The book was sold for 225 CZK and was sold out very quickly. The publishing house prepared a reprint and expanded the book with new photographs. The extended version of the book costs CZK 280. By what percentage is the new book more expensive? - Drill bit
Bill's 3/8-inch drill bit is missing and needed for a job. He can get by with drilling a smaller hole than 3/8-inch as long as it is as close to 3/8-inch as possible. Which of the following bits would be the best to use? A. 13/32 inch B. 23/64 inch C. 1/2 - The temperature 35
The temperature was -8 degrees at 10:00 in the morning. If the temperature rises 3 degrees per hour, what will the temperature be at 2:00 in the afternoon? - A car 6
A car holds 15 liters of fuel. The car consumes 3 liters of fuel each 100 km. We started a trip of 350 km with a full tank of fuel. How much fuel remains in the tank at the end of the trip? - Solve 16
Solve for the value of the variables x: y:30=3:21 - Peter 11
Peter is answering to ten word math problems. It takes him 1 ⅓ hour to answer five and 1 ½ hours to answer 5. On average, how many minutes does it take him to answer a problem? - Cuboid's diagonal
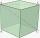The cuboid has a body diagonal u=25 cm, and side b is one-third longer than side a. What is the volume of the cuboid? - The point
The point which lies in the fourth quadrant is A.(2,1) B.(1,-3) C.( -5,-2) D. (-4,0) E. (0,0) - The midpoint 2
Find the value of x if M is the midpoint of PQ, PQ=10x−7, and PM=14. - Nicolette
Nicolette makes a small bead bracelet using five red, eight purple, and six green beads. A large necklace has the same ratio of beads as a small bracelet. If the large necklace requires 15 red beads, how many purple beads are needed to make a large bracel - A town 2
A town has raised 3/8 of the 12,000 and needs to furnish its new library. How much more money is it hoping to raise? - A solution
A solution of salt and water has 15% salt by weight. From it, 30 kg evaporated, and the solution now contains 20% salt. Find the original quantity of the solution. - Year salary
2/5 of a man's salary is 40,000. What is his salary? - Fencing
Ruby is purchasing fencing to go around a rectangular lot which is 4x + 9 feet long and 3x - 5 feet wide. Which expression represents the amount of fencing she must buy? - Two drops Between 5:00 pm to 6:00 pm, the temperature dropped 3°C. Between 6:00 pm to 7:00 pm, the temperature dropped 4°C. What was the total drop in temperature from 5:00 pm to 7:00 pm?
- Expression with powers
Which expression is equivalent to 2.1 raised to the fifth power divided by 0.9 raised to the fourth power, all raised to the third power? - Marbles 4
Sipho has a cylindrical tank with a radius of 8cm and a height of 10cm. The bottom of the tank is filled with marbles, and the tank is then filled with water to a height of 6,4 cm. When the marbles are removed, the water level drops to 4cm. Using the info
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
