Maths practice for 14 year olds - page 62 of 370
Number of problems found: 7397
- Through 80963
 The fire tank is filled with three inlets, each flowing 6 liters per second in 12 hours. How long will it take to fill if 8 liters per second flow through each of them?
The fire tank is filled with three inlets, each flowing 6 liters per second in 12 hours. How long will it take to fill if 8 liters per second flow through each of them? - Five-minute 80951
 Karel has an average grade of exactly 1.12 from five-minute episodes. Prove that at least 22 of them have one.
Karel has an average grade of exactly 1.12 from five-minute episodes. Prove that at least 22 of them have one. - The perimeter
 The perimeter of the base of a regular quadrilateral pyramid is the same as its height. The pyramid has a volume of 288 dm³. Calculate its surface area round the result to the whole dm².
The perimeter of the base of a regular quadrilateral pyramid is the same as its height. The pyramid has a volume of 288 dm³. Calculate its surface area round the result to the whole dm². - Elevation of the tower
 We can see the top of the tower standing on a plane from a certain point A at an elevation angle of 39°25''. If we come towards its foot 50m closer to place B, we can see the top of the tower from it at an elevation angle of 56°42''. How tall is the tower
We can see the top of the tower standing on a plane from a certain point A at an elevation angle of 39°25''. If we come towards its foot 50m closer to place B, we can see the top of the tower from it at an elevation angle of 56°42''. How tall is the tower - Interest 80867
 How much is the deposit? Which at an interest rate of 3.75%p. a., will it increase by 25 euros in one year?
How much is the deposit? Which at an interest rate of 3.75%p. a., will it increase by 25 euros in one year? - Temperature 80864
 You have water at a temperature of 10°C and boiling water at a temperature of 100°C. How do you prepare 9 liters of water at a temperature of 30°C?
You have water at a temperature of 10°C and boiling water at a temperature of 100°C. How do you prepare 9 liters of water at a temperature of 30°C? - Centimeters 80859
 Triangle ABC and triangle ADE are similar. Calculate in square centimeters the area of triangle ABC if the length of side DE is 12 cm, the length of side BC is 16 cm, and the area of triangle ADE is 27 cm².
Triangle ABC and triangle ADE are similar. Calculate in square centimeters the area of triangle ABC if the length of side DE is 12 cm, the length of side BC is 16 cm, and the area of triangle ADE is 27 cm². - Perimeter 80853
 The lengths of the sides of the triangle are in the ratio 7:6:4. The shortest side is 36 cm. What is the perimeter in cm of this triangle?
The lengths of the sides of the triangle are in the ratio 7:6:4. The shortest side is 36 cm. What is the perimeter in cm of this triangle? - Equilateral 80851
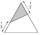 Kornelia cut off the colored part from the equilateral triangle. The shortest side of the colored triangle is 1/3 the length of the side of the original triangle. Calculate what part of the triangle she cut off.
Kornelia cut off the colored part from the equilateral triangle. The shortest side of the colored triangle is 1/3 the length of the side of the original triangle. Calculate what part of the triangle she cut off. - Purchase 80850
 Janka and Danka together paid €132 for the purchase. However, Jana paid five times more than Danka. How many euros did Janka pay, and how much did Danka pay?
Janka and Danka together paid €132 for the purchase. However, Jana paid five times more than Danka. How many euros did Janka pay, and how much did Danka pay? - Consumption 80836
 The right trapezoidal plot has a basic length of 102m and 86m. The vertical arm is 63 m long. Calculate the plot’s area and the mesh consumption for its fencing.
The right trapezoidal plot has a basic length of 102m and 86m. The vertical arm is 63 m long. Calculate the plot’s area and the mesh consumption for its fencing. - Longitudinal 80822
 How does the rail lengthen when the temperature changes from -30°C to 30°C if it is 25 m long at 0°C? The temperature coefficient of longitudinal expansion is 12.10na-6Kna-1.
How does the rail lengthen when the temperature changes from -30°C to 30°C if it is 25 m long at 0°C? The temperature coefficient of longitudinal expansion is 12.10na-6Kna-1. - Transported 80813
 Three Tatras transported 22.2 tons of sand. The second Tatra transported 20% more than the first, and the third Tatra 25% more than the second. How much did each Tatra take?
Three Tatras transported 22.2 tons of sand. The second Tatra transported 20% more than the first, and the third Tatra 25% more than the second. How much did each Tatra take? - Manufacturer 80810
 The manufacturer indicates that the germination rate of the pepper seeds is 68%. What is the probability that a) out of ten seeds sown, at least 8 will germinate? b) will at most 3 sprouts out of ten seeds be sown?
The manufacturer indicates that the germination rate of the pepper seeds is 68%. What is the probability that a) out of ten seeds sown, at least 8 will germinate? b) will at most 3 sprouts out of ten seeds be sown? - Trapezoid roof
 The house's roof is a trapezoid of the same name, with 85 tiles at the ridge and 100 tiles at the bottom. There is always one more tiles in each row than the previous one. How many tiles do I need for the entire roof?
The house's roof is a trapezoid of the same name, with 85 tiles at the ridge and 100 tiles at the bottom. There is always one more tiles in each row than the previous one. How many tiles do I need for the entire roof? - Discount 80806
 Price before discount 250, after discount 200. Find discount by n% and discount to n%.
Price before discount 250, after discount 200. Find discount by n% and discount to n%. - Delivering 80805
 The courier company delivers the ordered goods through the e-shop. If the delivery were made by 2 cars, it would be completed in 6 hours. However, after 4 hours, the first car's driver stopped delivering, and the second car continued to deliver for anothe
The courier company delivers the ordered goods through the e-shop. If the delivery were made by 2 cars, it would be completed in 6 hours. However, after 4 hours, the first car's driver stopped delivering, and the second car continued to deliver for anothe - Calculate 80804
 The school bought 20 tablets and 15 laptops for the students for a total of exactly €6,000. Calculate the amount of one tablet and the price of a laptop if the tablet was €50 cheaper than the laptop.
The school bought 20 tablets and 15 laptops for the students for a total of exactly €6,000. Calculate the amount of one tablet and the price of a laptop if the tablet was €50 cheaper than the laptop. - Multiply 80797
 When I multiply two equal natural numbers, I get the same result as when I add them together. Which ones are they?
When I multiply two equal natural numbers, I get the same result as when I add them together. Which ones are they? - Apple 80796
 A total of 18 pear and apple trees grow in the set. Pears are 2 times less than apple trees. How many pears and apple trees are there?
A total of 18 pear and apple trees grow in the set. Pears are 2 times less than apple trees. How many pears and apple trees are there?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
