Angle - practice problems - page 2 of 64
Number of problems found: 1269
- Two men 2
 Two men are on opposite sides of a tower. They measure the angles of elevation of the top of the tower as 30° and 45°, respectively. If the height of the tower is 50 m, find the distance between the two men.
Two men are on opposite sides of a tower. They measure the angles of elevation of the top of the tower as 30° and 45°, respectively. If the height of the tower is 50 m, find the distance between the two men. - RT with rectangle
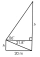 In the diagram, find the lengths h and b. One rectangle and one right triangle share one side. We know two angles and the length of the common side, as shown in the picture.
In the diagram, find the lengths h and b. One rectangle and one right triangle share one side. We know two angles and the length of the common side, as shown in the picture. - The supplement
 The supplement of an angle is four times its complement. Find the angle.
The supplement of an angle is four times its complement. Find the angle. - Minimum interior angle
 What is the minimum interior angle possible for a regular polygon?
What is the minimum interior angle possible for a regular polygon? - Hands of a clock
 At what time between 11 and 12 O'clock will the hands of a clock be at an angle of 180°?
At what time between 11 and 12 O'clock will the hands of a clock be at an angle of 180°? - Elevation angle
 A man standing on the deck of a ship, which is 10 m above the water level, observes the angle of elevation of the top of a hill as 60°, and angle of depression of the base of the hill is 30°. Find the distance of the hill from the ship and the height of t
A man standing on the deck of a ship, which is 10 m above the water level, observes the angle of elevation of the top of a hill as 60°, and angle of depression of the base of the hill is 30°. Find the distance of the hill from the ship and the height of t - Interior angles 4
 How many degrees are in the sum of the interior angles of a quadrilateral?
How many degrees are in the sum of the interior angles of a quadrilateral? - Quadrilateral angles in AP
 The four angles of a quadrilateral form an arithmetic progression. If the common difference is 15°, then find all the angles.
The four angles of a quadrilateral form an arithmetic progression. If the common difference is 15°, then find all the angles. - Number of sides
 Find the number of sides of a regular polygon whose each exterior angle has a measure of 45°.
Find the number of sides of a regular polygon whose each exterior angle has a measure of 45°. - Tuesday temperature
 The temperature on Monday was -23°F. The temperature on Tuesday was 18° higher. What was the temperature on Tuesday?
The temperature on Monday was -23°F. The temperature on Tuesday was 18° higher. What was the temperature on Tuesday? - Angle of elevation
 The angle of elevation of the top of an unfinished pillar at a point 150 m from its base is 30°. If the angle of elevation at the same point is to be 45°, then the pillar has to be raised to a height of how many meters?
The angle of elevation of the top of an unfinished pillar at a point 150 m from its base is 30°. If the angle of elevation at the same point is to be 45°, then the pillar has to be raised to a height of how many meters? - Two vertically
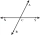 Two vertically opposite angles are (x-20)° and 85°; then, find the value of x.
Two vertically opposite angles are (x-20)° and 85°; then, find the value of x. - Central angle 2
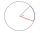 What is the arc length of a circle with a radius of 12 cm and a central angle of 255 degrees? A. 8.5 cm B. 12π cm C. 24π cm D. 17π cm
What is the arc length of a circle with a radius of 12 cm and a central angle of 255 degrees? A. 8.5 cm B. 12π cm C. 24π cm D. 17π cm - The tent 3
 The top of a 1.3 meters tall tent is tethered to the ground by a cable. The cable makes a 37 degrees angle with the ground. Find the cable length.
The top of a 1.3 meters tall tent is tethered to the ground by a cable. The cable makes a 37 degrees angle with the ground. Find the cable length. - Two angles
 If one angle of a parallelogram is 24° less than twice the smallest angle, then find the largest angle of the parallelogram.
If one angle of a parallelogram is 24° less than twice the smallest angle, then find the largest angle of the parallelogram. - At 5:16
 At 5:16, what is the acute angle between a minute hand and an hour hand?
At 5:16, what is the acute angle between a minute hand and an hour hand? - Parallelogram - right angles
 In parallelogram ABCD; AB = 16 cm, BC = 12 cm and diagonal AC = 20 cm. Find the area of the parallelogram.
In parallelogram ABCD; AB = 16 cm, BC = 12 cm and diagonal AC = 20 cm. Find the area of the parallelogram. - The reflection law
 AB is a mirror, PQ is the incident ray, and QR is the reflected ray. If angle PQR = 112°, find angle PQA.
AB is a mirror, PQ is the incident ray, and QR is the reflected ray. If angle PQR = 112°, find angle PQA. - Complement and supplement
 Find the measure of an angle if 7 times its complement is 10° less than 3 times its supplement.
Find the measure of an angle if 7 times its complement is 10° less than 3 times its supplement. - An electrician 7
 An electrician has to repair an electric fault on a pole 4 meters in height. He needs to reach a point 1 m below the top. What should be the length of the ladder that he could use, when inclined at an angle 60° to the horizontal?
An electrician has to repair an electric fault on a pole 4 meters in height. He needs to reach a point 1 m below the top. What should be the length of the ladder that he could use, when inclined at an angle 60° to the horizontal?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
