Sine + angle - practice problems
Number of problems found: 262
- X-triangle
 Find the length of the x segment in the given triangle drawings.
Find the length of the x segment in the given triangle drawings. - Trigonometric fx
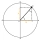 When an acute angle φ is in the standard position, its terminal side passes through point P (1,3). Find trigonometric functions of angle θ : sin φ, cos φ, tan φ, cotan φ.
When an acute angle φ is in the standard position, its terminal side passes through point P (1,3). Find trigonometric functions of angle θ : sin φ, cos φ, tan φ, cotan φ. - Three 235
 Three houses form a triangular shape. House A is 50 feet from house C and house B is 60 feet from house C. The measure is angle ABC is 80 degrees. Draw a picture and find the distance between A and B.
Three houses form a triangular shape. House A is 50 feet from house C and house B is 60 feet from house C. The measure is angle ABC is 80 degrees. Draw a picture and find the distance between A and B. - Subtract polar forms
 Solve the following 5.2∠58° - 1.6∠-40° and give answer in polar form
Solve the following 5.2∠58° - 1.6∠-40° and give answer in polar form
- Conjugate coordinates
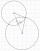 If the rectangular conjugate of the polar vector 12 angle 35 degrees is equal to x+yi, find the sum of x and y.
If the rectangular conjugate of the polar vector 12 angle 35 degrees is equal to x+yi, find the sum of x and y. - Let z 2
 Let z = 2 - sqrt(3i). Find z6 and express your answer in rectangular form. if z = 2 - 2sqrt(3 i) then r = |z| = sqrt(2 ^ 2 + (- 2sqrt(3)) ^ 2) = sqrt(16) = 4 and theta = tan -2√3/2=-π/3
Let z = 2 - sqrt(3i). Find z6 and express your answer in rectangular form. if z = 2 - 2sqrt(3 i) then r = |z| = sqrt(2 ^ 2 + (- 2sqrt(3)) ^ 2) = sqrt(16) = 4 and theta = tan -2√3/2=-π/3 - Isosceles 83247
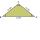 Calculate the lengths of the sides in an isosceles triangle, given the height (to the base) Vc= 8.8cm and the angle at the base alpha= 38°40`.
Calculate the lengths of the sides in an isosceles triangle, given the height (to the base) Vc= 8.8cm and the angle at the base alpha= 38°40`. - Subtended 83194
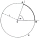 A circle k with a center at point S and a radius of 6 cm is given. Calculate the size of the central angle subtended by a chord 10 cm long.
A circle k with a center at point S and a radius of 6 cm is given. Calculate the size of the central angle subtended by a chord 10 cm long. - Determine 83081
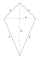 A paper kite is shaped like a deltoid ABCD, with two shorter sides 30 cm long, two longer sides 51 cm long, and a shorter diagonal 48 cm long. Determine the sizes of the internal angles of the given deltoid.
A paper kite is shaped like a deltoid ABCD, with two shorter sides 30 cm long, two longer sides 51 cm long, and a shorter diagonal 48 cm long. Determine the sizes of the internal angles of the given deltoid.
- Inaccessible 82710
 Determine the distance between two inaccessible places K, L, if the angles KAL=62°10", LAB=41°23", KBL=66°34", and LBA were measured from points A, B, which are 870 m apart = 34°52". Thank you.
Determine the distance between two inaccessible places K, L, if the angles KAL=62°10", LAB=41°23", KBL=66°34", and LBA were measured from points A, B, which are 870 m apart = 34°52". Thank you. - Observatories 82707
 Target C is observed from two artillery observatories, A and B, 296m apart. At the same time, angle BAC = 52°42" and angle ABC = 44°56". Calculate the distance of the target from observatory A.
Target C is observed from two artillery observatories, A and B, 296m apart. At the same time, angle BAC = 52°42" and angle ABC = 44°56". Calculate the distance of the target from observatory A. - Parallelogram 82695
 Given is the parallelogram KLMN, in which we know the side sizes/KL/ = a = 84.5 cm, /KN/ = 47.8 cm, and the angle size at the vertex K 56°40'. Calculate the size of the diagonals.
Given is the parallelogram KLMN, in which we know the side sizes/KL/ = a = 84.5 cm, /KN/ = 47.8 cm, and the angle size at the vertex K 56°40'. Calculate the size of the diagonals. - Circular 82418
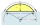 A circular segment has an area of 6.04 cm², the central omega angle is 15 degrees, what is the radius?
A circular segment has an area of 6.04 cm², the central omega angle is 15 degrees, what is the radius? - Determine 82032
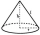 Determine the volume and surface area of a cone whose slope of length 8 cm makes an angle of 75 degrees with the plane of the base.
Determine the volume and surface area of a cone whose slope of length 8 cm makes an angle of 75 degrees with the plane of the base.
- Calculate 81950
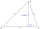 The tangent of the angle formed by the adjacent sides of the triangle ABC (side a=29 m, b = 40 m) equals 1.05. Calculate the area of that triangle.
The tangent of the angle formed by the adjacent sides of the triangle ABC (side a=29 m, b = 40 m) equals 1.05. Calculate the area of that triangle. - Difference 81888
 The ropeway climbs at an angle of 22°30'. Calculate its length if the height difference between the lower and upper station is 560m. Sketch a picture
The ropeway climbs at an angle of 22°30'. Calculate its length if the height difference between the lower and upper station is 560m. Sketch a picture - Perpendicular 81758
 Distribute the force of magnitude F = 100 N into two perpendicular components with magnitudes F1 and F2 so that the angle between forces F1 and F is 43°52'.
Distribute the force of magnitude F = 100 N into two perpendicular components with magnitudes F1 and F2 so that the angle between forces F1 and F is 43°52'. - Archaeologists 81478
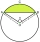 Archaeologists need to find out the size of the vessel if the sherd found was in the shape of a circular section with a length of 12 cm and a height of 3 cm. What is the area of this section?
Archaeologists need to find out the size of the vessel if the sherd found was in the shape of a circular section with a length of 12 cm and a height of 3 cm. What is the area of this section? - Quadrilateral 81097
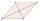 The quadrilateral ABCD is symmetrical about the diagonal AC. The length of AC is 12 cm, the length of BC is 6 cm, and the interior angle at vertex B is right. points E and F are given on the sides AB, and AD so that the triangle ECF is equilateral. Determ
The quadrilateral ABCD is symmetrical about the diagonal AC. The length of AC is 12 cm, the length of BC is 6 cm, and the interior angle at vertex B is right. points E and F are given on the sides AB, and AD so that the triangle ECF is equilateral. Determ
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
