Examples of area of plane shapes - page 37 of 131
Number of problems found: 2605
- Playground
 On the special playground, there are 81 square sectors, each with a side of 5 m. How many players can fit on the playground if each player needs a 75 m² area to play?
On the special playground, there are 81 square sectors, each with a side of 5 m. How many players can fit on the playground if each player needs a 75 m² area to play? - Production 7636
 The production of kites requires 12 square meters. The paper is 125 cm wide. How many meters of paper do we need to buy?
The production of kites requires 12 square meters. The paper is 125 cm wide. How many meters of paper do we need to buy? - Area of a circle
 The circumference of the circle is 150.72 centimeters. Calculate the area of the circle.
The circumference of the circle is 150.72 centimeters. Calculate the area of the circle. - Corresponding 5386
 A football field for an interstate match must be between 100 m and 110 m long and between 64 m and 75 m wide. Calculate the area of the smallest and largest fields corresponding to the conditions.
A football field for an interstate match must be between 100 m and 110 m long and between 64 m and 75 m wide. Calculate the area of the smallest and largest fields corresponding to the conditions. - Circumference 4421
 The area of an equilateral triangle is 81 times three below the square root of cm². Calculate its circumference.
The area of an equilateral triangle is 81 times three below the square root of cm². Calculate its circumference. - Rectangle 4077
 We cut the largest possible circle from a paper rectangle with 25 cm and 15 cm sides. How many % of the area of the rectangle is the area of the circle?
We cut the largest possible circle from a paper rectangle with 25 cm and 15 cm sides. How many % of the area of the rectangle is the area of the circle? - Squares
 Calculate the area of the square and result round to square decimeters. a) a = 1,52 dm b) a = 13 268mm c) a = 562 cm d) a = 1,52 m
Calculate the area of the square and result round to square decimeters. a) a = 1,52 dm b) a = 13 268mm c) a = 562 cm d) a = 1,52 m - Trapezoid - legs
 Determine the trapezoid area with bases 84 and 47; the height is 4 shorter than its leg.
Determine the trapezoid area with bases 84 and 47; the height is 4 shorter than its leg. - Circles 2
 Calculate the area bounded by the circumscribed and inscribed circle in a triangle with sides 29 cm, 16 cm, and 21 cm.
Calculate the area bounded by the circumscribed and inscribed circle in a triangle with sides 29 cm, 16 cm, and 21 cm. - Calculate 3987
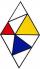 The diamond has an area of 94.24 square meters and one diagonal of 7.6 cm. Calculate the length of the second diagonal.
The diamond has an area of 94.24 square meters and one diagonal of 7.6 cm. Calculate the length of the second diagonal. - Parallelogram 44
 Parallelogram ABCD has an area of 32 cm2, lABl=8cm, lBCl=5cm. Calculate the sizes of its interior angles.
Parallelogram ABCD has an area of 32 cm2, lABl=8cm, lBCl=5cm. Calculate the sizes of its interior angles. - Nikelin and brass
 Calculate the length of brass wire (ró=0.08 microohm m) and nickel (ró=0.4 microohm m) with a diameter of 0.5 mm, which has a resistance of 1 ohm
Calculate the length of brass wire (ró=0.08 microohm m) and nickel (ró=0.4 microohm m) with a diameter of 0.5 mm, which has a resistance of 1 ohm - Rafael
 Rafael has three squares. The first square has a side length of 2 cm. The second square has a side length of 4 cm, and its vertex is placed in the center of the first square. The last square has a side length of 6 cm, and its vertex is placed in the cente
Rafael has three squares. The first square has a side length of 2 cm. The second square has a side length of 4 cm, and its vertex is placed in the center of the first square. The last square has a side length of 6 cm, and its vertex is placed in the cente - Isosceles right triangle
 If the square of the hypotenuse of an isosceles right triangle is 128 cm2, find the length of each side.
If the square of the hypotenuse of an isosceles right triangle is 128 cm2, find the length of each side. - Circular segment
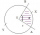 Calculate the radius and area of the circular segment if the center angle = 106° and the length of the corresponding circular arc is l = 52 cm.
Calculate the radius and area of the circular segment if the center angle = 106° and the length of the corresponding circular arc is l = 52 cm. - Circle segment
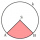 A quarter circle with a radius of 4 has the same area as a circle segment with a radius of 3. What is the magnitude of the center angle of the circle segment?
A quarter circle with a radius of 4 has the same area as a circle segment with a radius of 3. What is the magnitude of the center angle of the circle segment? - Flowerbeds
 There are three square flower beds on the square grassy plot. What percentage is the grassed part of the land when one side is 35 m, and the side of the flowerbed is 10 m?
There are three square flower beds on the square grassy plot. What percentage is the grassed part of the land when one side is 35 m, and the side of the flowerbed is 10 m? - Center of gravity and median
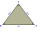 In the isosceles triangle ABC, the center of gravity T is 2 cm from the base AB. The median parallel to the AB side measures 4 cm. What is the area of the ABC triangle?
In the isosceles triangle ABC, the center of gravity T is 2 cm from the base AB. The median parallel to the AB side measures 4 cm. What is the area of the ABC triangle? - Rectangular land
 Due to the new road, the longer dimension of the rectangular plot had to be shortened by 4 percent, and the shorter dimension shrunk by 10 percent. Thus, the area of the land has decreased by how much percent?
Due to the new road, the longer dimension of the rectangular plot had to be shortened by 4 percent, and the shorter dimension shrunk by 10 percent. Thus, the area of the land has decreased by how much percent? - Parallelogram - A+p
 Calculate the area and perimeter of a parallelogram if side a = 5.2 cm and height to side is va = 4 cm (it is a parallelogram, not a triangle)
Calculate the area and perimeter of a parallelogram if side a = 5.2 cm and height to side is va = 4 cm (it is a parallelogram, not a triangle)
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
