Three altitudes

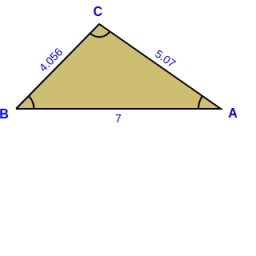
A triangle with altitudes 4; 5 and 6 cm is given. Calculate the lengths of all medians and all sides in a triangle.

Result

a =  7.524 cm
b =  6.019 cm
c =  5.016 cm
t1 =  4.067 cm
t2 =  5.642 cm
t3 =  6.335 cm

Solution:

v1=4 cm v2=5 cm v3=6 cm  h=1/v1+1/v2+1/v32=1/4+1/5+1/62≐37120≐0.3083 t=h⋅ (h−1/v1)⋅ (h−1/v2)⋅ (h−1/v3)=0.3083⋅ (0.3083−1/4)⋅ (0.3083−1/5)⋅ (0.3083−1/6)≐0.0003  s=4⋅ t=4⋅ 0.0003≐0.0665 S=1s=10.0665≐15.0472 cm2  S=a⋅ v12  a=2⋅ S/v1=2⋅ 15.0472/4≐7.5236≐7.524 cmv_{1}=4 \ \text{cm} \ \\ v_{2}=5 \ \text{cm} \ \\ v_{3}=6 \ \text{cm} \ \\ \ \\ h=\dfrac{ 1/v_{1}+1/v_{2}+1/v_{3} }{ 2 }=\dfrac{ 1/4+1/5+1/6 }{ 2 } \doteq \dfrac{ 37 }{ 120 } \doteq 0.3083 \ \\ t=h \cdot \ (h-1/v_{1}) \cdot \ (h-1/v_{2}) \cdot \ (h-1/v_{3})=0.3083 \cdot \ (0.3083-1/4) \cdot \ (0.3083-1/5) \cdot \ (0.3083-1/6) \doteq 0.0003 \ \\ \ \\ s=4 \cdot \ \sqrt{ t }=4 \cdot \ \sqrt{ 0.0003 } \doteq 0.0665 \ \\ S=\dfrac{ 1 }{ s }=\dfrac{ 1 }{ 0.0665 } \doteq 15.0472 \ \text{cm}^2 \ \\ \ \\ S=\dfrac{ a \cdot \ v_{1} }{ 2 } \ \\ \ \\ a=2 \cdot \ S/v_{1}=2 \cdot \ 15.0472/4 \doteq 7.5236 \doteq 7.524 \ \text{cm}

Try calculation via our triangle calculator.

b=2⋅ Sv2=2⋅ 15.04725≐6.0189≐6.019 cmb=\dfrac{ 2 \cdot \ S }{ v_{2} }=\dfrac{ 2 \cdot \ 15.0472 }{ 5 } \doteq 6.0189 \doteq 6.019 \ \text{cm}
c=2⋅ Sv3=2⋅ 15.04726≐5.0157≐5.016 cmc=\dfrac{ 2 \cdot \ S }{ v_{3} }=\dfrac{ 2 \cdot \ 15.0472 }{ 6 } \doteq 5.0157 \doteq 5.016 \ \text{cm}
t1=2⋅ b2+2⋅ c2−a22=2⋅ 6.01892+2⋅ 5.01572−7.523622≐4.0671≐4.067 cmt_{1}=\dfrac{ \sqrt{ 2 \cdot \ b^2+2 \cdot \ c^2-a^2 } }{ 2 }=\dfrac{ \sqrt{ 2 \cdot \ 6.0189^2+2 \cdot \ 5.0157^2-7.5236^2 } }{ 2 } \doteq 4.0671 \doteq 4.067 \ \text{cm}
t2=2⋅ a2+2⋅ c2−b22=2⋅ 7.52362+2⋅ 5.01572−6.018922≐5.6417≐5.642 cmt_{2}=\dfrac{ \sqrt{ 2 \cdot \ a^2+2 \cdot \ c^2-b^2 } }{ 2 }=\dfrac{ \sqrt{ 2 \cdot \ 7.5236^2+2 \cdot \ 5.0157^2-6.0189^2 } }{ 2 } \doteq 5.6417 \doteq 5.642 \ \text{cm}
t3=2⋅ a2+2⋅ b2−c22=2⋅ 7.52362+2⋅ 6.01892−5.015722≐6.3348≐6.335 cmt_{3}=\dfrac{ \sqrt{ 2 \cdot \ a^2+2 \cdot \ b^2-c^2 } }{ 2 }=\dfrac{ \sqrt{ 2 \cdot \ 7.5236^2+2 \cdot \ 6.0189^2-5.0157^2 } }{ 2 } \doteq 6.3348 \doteq 6.335 \ \text{cm}

Try another example


Our examples were largely sent or created by pupils and students themselves. Therefore, we would be pleased if you could send us any errors you found, spelling mistakes, or rephasing the example. Thank you!





Leave us a comment of this math problem and its solution (i.e. if it is still somewhat unclear...):

Showing 0 comments:
1st comment
Be the first to comment!
avatar




Tips to related online calculators
Looking for calculator of harmonic mean?
Looking for a statistical calculator?
Do you have a linear equation or system of equations and looking for its solution? Or do you have quadratic equation?
Do you want to convert length units?
See also our trigonometric triangle calculator.
Pythagorean theorem is the base for the right triangle calculator.

You need to know the following knowledge to solve this word math problem:


 
We encourage you to watch this tutorial video on this math problem: video1   video2

Next similar math problems:

  1. Theorem prove
    thales_1 We want to prove the sentence: If the natural number n is divisible by six, then n is divisible by three. From what assumption we started?
  2. Calculate
    equilateral_triangle2 Calculate the length of a side of the equilateral triangle with an area of 50cm2.
  3. Isosceles triangle 9
    iso_triangle Given an isosceles triangle ABC where AB= AC. The perimeter is 64cm and altitude is 24cm. Find the area of the isosceles triangle
  4. Trapezoid
    lichobeznik_3 trapezoid ABCD a = 35 m, b=28 m c = 11 m and d = 14 m. How to calculate its area?
  5. Thunderstorm
    blesk The height of the pole before the storm is 10 m. After a storm when they come to check it they see that on the ground from the pole blows part of the column. Distance from the pole is 3 meters. At how high was the pole broken? (In fact, a rectangular tri
  6. Intercept with axis
    log_10 F(x)=log(x+4)-2, what is the x intercept
  7. Parametric equation
    line Find the parametric equation of a line with y-intercept (0,-4) and a slope of -2.
  8. Linear imaginary equation
    cplx_function Given that ? "this is z star" Find the value of the complex number z.
  9. Add vector
    vectors_2 Given that P = (5, 8) and Q = (6, 9), find the component form and magnitude of vector PQ.
  10. Difference AP 4
    sequence_geo_1 Calculate the difference of the AP if a1 = 0.5, a2 + a3 = -1.1
  11. Harmonic and arithmetic means
    Plot_harmonic_mean The local Utah Department of Child Service office wants to project staffing needs based on current social worker assignments. They have the number of cases per social worker for the following staff: Mary: 25 John: 35 Ted: 15 Lisa: 45 Anna: 20 Calcula
  12. Crystal water
    laboratory The chemist wanted to check the content of water of crystallization of chromic potassium alum K2SO4 * Cr2 (SO4) 3 * 24 H2O, which was a long time in the laboratory. From 96.8 g of K2SO4 * Cr2 (SO4) 3 * 24 H2O prepared 979 cm3 solution of base.
  13. Square root 2
    parabola_2 If the square root of 3m2 +22 and -x = 0, and x=7, what is m?
  14. Equation 23
    reciprocal_1 Find value of unknown x in equation: x+3/x+1=5 (problem finding x)
  15. Evaluation of expressions
    eq222_10 If a2-3a+1=0, find (i)a2+1/a2 (ii) a3+1/a3
  16. GP members
    sequence_geo_8 The geometric sequence has 10 members. The last two members are 2 and -1. Which member is -1/16?
  17. Ball game
    lopta_3 Richard, Denis and Denise together scored 932 goals. Denis scored 4 goals over Denise but Denis scored 24 goals less than Richard. Determine the number of goals for each player.