Medians and sides
Triangle ABC in the plane Oxy; are the coordinates of the points:
A = 2.7
B = -4.3
C-6-1
Try to calculate the lengths of all medians and all sides.
A = 2.7
B = -4.3
C-6-1
Try to calculate the lengths of all medians and all sides.
Correct answer:
Tips for related online calculators
Our vector sum calculator can add two vectors given by their magnitudes and by included angle.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Coordinates of a centroind
Let’s A = [3, 2, 0], B = [1, -2, 4] and C = [1, 1, 1] be 3 points in space. Calculate the coordinates of the centroid of △ABC (the intersection of the medians). - Lengths of medians from coordinates
There is a triangle ABC: A [-6.6; 1.2], B [3.4; -5.6], C [2.8; 4.2]. Calculate the lengths of its medians. - Three altitudes
A triangle with altitudes 4, 5, and 6 cm is given. Calculate the lengths of all medians and all sides in a triangle. - The triangles
Two similar triangles, KLM and ABC, are given. Calculate the lengths of the remaining sides of the triangle KLM. If the lengths of the sides are a = 7 b = 5.6 c = 4.9 k = 5 - Calculate 72624
The perimeter of the ABC triangle is 19.6 cm. The following applies to the lengths of its sides: a: c = 1:2, b: c = 5:6. Calculate the lengths of all sides of the triangle ABC. - Medians in RT
The rectangular triangle ABC has a length of 10 cm and 24 cm. Points P, Q, and R are the centers of the sides of this triangle. The perimeter of the PQR triangle is: - Triangle's centroid
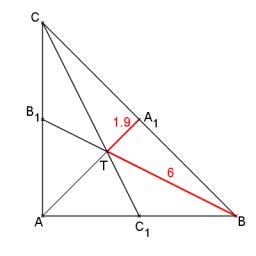
In the triangle ABC the given lengths of its medians tc = 9, ta = 6. Let T be the intersection of the medians (triangle's centroid), and the point S is the center of the side BC. The magnitude of the CTS angle is 60°. Calculate the length of the BC side t - Coordinates of the vertices
Calculate the coordinates of the vertices of a triangle if the equations of its sides are 7x-4y-1 = 0 x-2y + 7 = 0 2x + y + 4 = 0 - Perimeter 66414
The perimeter of triangle ABC is 162 dm. The lengths of its sides are in the ratios a:b = 2:3 and a:c = 8:7. Determine the lengths of the sides of the triangle. - Similar triangles
The triangles ABC and XYZ are similar. Find the missing lengths of the sides of the triangles. a) a = 5 cm b = 8 cm x = 7.5 cm z = 9 cm b) a = 9 cm c = 12 cm y = 10 cm z = 8 cm c) b = 4 cm c = 8 cm x = 4.5 cm z = 6 cm - Medians and sides
Determine the size of a triangle KLM and the size of the medians in the triangle. K=(-5; -6), L=(7; -2), M=(5; 6). - Right-angled 81019
In the right-angled triangle ABC (AB is the hypotenuse), a : b = 24 : 7, and the height to the side c = 12.6 cm applies. Calculate the lengths of the sides of triangle ABC. - Median
In the right triangle are sides a=96 dm b=31 dm. Calculate the length of the medians tc to the hypotenuse. - Coordinates 32183
The triangle ABC is given in the plane. A (-3,5), B (2,3), C (-1, -2) write the coordinates of the vectors u, v, w if u = AB, v = AC, and w = BC. Enter the coordinates of the centers of the lines SAB (..), SAC (...), SBC (. ..) - Triangle ABC
In a triangle ABC with the side BC of length 2 cm. Point K is the middle point of AB. Points L and M split the AC side into three equal lines. KLM is an isosceles triangle with a right angle at point K. Determine the lengths of the sides AB, AC triangle A - Rectangular triangles
The lengths of corresponding sides of two rectangular triangles are in the ratio 2:5. At what ratio are medians relevant to hypotenuse these right triangles? At what ratio are the areas of these triangles? A smaller rectangular triangle has legs 6 and 8 c - Angles and sides of the triangle
Triangle ABC has a circumference of 26 cm. Lengths of the sides are as follows: a = 11.2 cm; b = 6.5 cm. Arrange the interior angles in order of their size. ...
