Těžnice
Trojúhelník ABC v rovině Oxy; jsou dány souřadnice bodů:
A = 2,7
B = -4,3
C = 6, -1
Zkuste vypočítet všechny těžnice a všechny délky stran.
Vaše odpověď:
A = 2,7
B = -4,3
C = 6, -1
Zkuste vypočítet všechny těžnice a všechny délky stran.
Vaše odpověď:
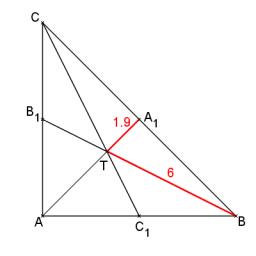
Tipy na související online kalkulačky
Dva vektory určeny velikostmi a vzájemným úhlem sčítá naše kalkulačka sčítání vektorů .
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
geometriearitmetikaplanimetrieÚroveň náročnosti úkolu
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Souřadnice vektorů a středů
V rovině je dán trojúhelník ABC. A(-3,5), B(2,3), C(-1,-2) zapište souřadnice vektorů u, v, w pokud u=AB, v=AC, w=BC. Zapište souřadnice středů úseček SAB(. .), SAC(. .. ), SBC(. .. ) - Obvod trojúhelníku ABT
V trojúhelníku ABC je dána strana c=5 cm a těžnice ta=6 cm, tb=4,5 cm. Vypočítá obvod trojúhelníku ABT (T= těžiště). - Těžiště
Těžiště trojúhelníku ABC je v bodě (3,3,3). Pokud jsou souřadnice bodů A a B (3, –5, 7) a (–1, 7, – 6), najděte souřadnice bodu C. - Těžnice 10
Je dána úsečka AA1 délky 6 cm. Sestrojte všechny trojúhelníky ABC, pro které je AA1 těžnicí, délka strany BC je 5 cm a velikost úhlu gama je 60°. - Trojúhelníky
Dané jsou trojúhelníky KLM a ABC, které jsou navzájem podobné. Dopočítaj délky zbývajících stran trojúhelníku KLM, ka délky tran jsou a = 7 b = 5,6 c = 4,9 k = 5 - Ťežišťe a obsah
V trojúhelníku ABC jsou dány délky jeho těžnic tc = 9, ta = 6. Označme T průsečík těžnic, S střed strany BC. Velikost úhlu CTS je 60°. Vypočítejte délku strany BC s přesností na 2 desetinná místa. - Těžnice tc
V pravoúhlém trojúhelníku ABC su dané délky odvěsen a = 15 cm b = 36 cm. Vypočítejte délku těžnice tc.
