Strany a ťažnice
Trojuholník ABC v rovine Oxy; sú dané súradnice bodov:
A = 2,7
B = -4,3
C = 6, -1
Skúste vypočítať všetky ťažnice a všetky dĺžky strán.
Vaša odpoveď:
A = 2,7
B = -4,3
C = 6, -1
Skúste vypočítať všetky ťažnice a všetky dĺžky strán.
Vaša odpoveď:
Tipy na súvisiace online kalkulačky
Dva vektory určené veľkosťami a vzájomným uhlom sčíta naša kalkulačka sčítania vektorov.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
geometriaaritmetikaplanimetriaÚroveň náročnosti úlohy
Súvisiace a podobné príklady:
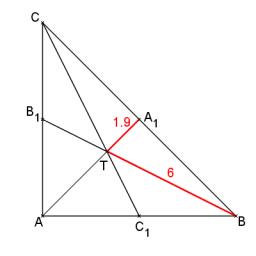
- V pravouhlom 6
V pravouhlom trojuholniku ABC sú dané dĺžky odvesien a=15 cm b=36 cm. Vypočítaj dĺžku ťažnice tc. - Dané sú 2
Dané sú trojuholníky KLM a ABC, ktoré sú navzájom podobné. Dopočítaj dĺžky zvyšných strán trojuholníka KLM, ka dĺžky trán sú a=7 b=5,6 c=4,9 k=5 - Trojuholník KLM
Dané sú body K( -3; 2), L(-1; 4), M(3, -4). Zistite: a) či je trojuholník KLM pravouhlý b) vypočítajte dĺžku ťažnice na stranu k c) napíšte súradnice vektora LM d) napíšte smernicový tvar strany KM e) napíšte smernicový tvar osi strany KM - Súradnice stran, výsek, osí
Je daný trojuholník ABC: A (-2,3), B (4, -1), C (2,5). Určte všeobecné rovnice priamok, na ktorých ležia,: a) strana AB, b) výška Vc, c) Os strany AB, d) Ťažnice ta - Ťažnice v PT
V pravouhlom trojuholníku ABC s pravým uhlom pri vrchole C sú dané veľkosti ťažníc ta=5, tb=2√10. Vypočítajte veľkosti strán trojuholníka ABC a polomer kružnice opísanej tomuto trojuholníku. - Ťažisko
Ťažisko trojuholníka ABC je v bode (3,3,3). Ak sú súradnice bodov A a B (3, –5, 7) a (–1, 7, – 6), nájdite súradnice bodu C. - V rovine
V rovine je daný trojuholník ABC. A(-3,5), B(2,3), C(-1,-2) zapíšte súradnice vektorov u, v, w ak u=AB, v=AC, w=BC. Zapíšte súradnice stredov úsečiek SAB(. .), SAC(. .. ), SBC(. .. )
