Triangle perimeter ratio
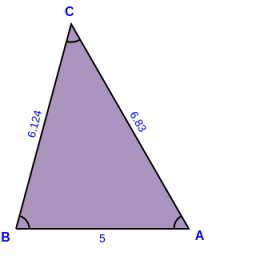
The perimeter of the ABC triangle is 19.6 cm. The following applies to the lengths of its sides: a: c = 1:2, b: c = 5:6. Calculate the lengths of all sides of the triangle ABC.
Your answer:
Your answer:
Tips for related online calculators
Need help calculating a sum, simplifying, or multiplying fractions? Try our fraction calculator.
Check out our ratio calculator.
See also our trigonometric triangle calculator.
Check out our ratio calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
algebraplanimetrybasic operations and conceptsnumbersGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Triangle height ratio
In the right-angled triangle ABC (AB is the hypotenuse), a : b = 24 : 7, and the height to the side c = 12.6 cm applies. Calculate the lengths of the sides of triangle ABC. - Medians and sides
Triangle ABC in the plane Oxy has the coordinates of the points: A = 2.7 B = -4.3 C-6-1 Try to calculate the lengths of all medians and all sides. - The triangle - sides
The two sides of the triangle have side lengths a = 6 cm and b = 13 cm. Then the following applies to the length of the third side c: (A) 7 - Triangle perimeter ratio
The perimeter of triangle ABC is 162 dm. The lengths of its sides are in the ratios a:b = 2:3 and a:c = 8:7. Determine the lengths of the sides of the triangle. - Angles and sides of the triangle
Triangle ABC has a circumference of 26 cm. The sides' lengths are as follows: a = 11.2 cm; b = 6.5 cm. Arrange the interior angles according to their size. - Triangle side calculation
Calculate the lengths of the remaining sides of right triangle ABC, given angle alpha = 45° and perimeter o = 125. - The triangles
Two similar triangles, KLM and ABC, are given. Calculate the lengths of the remaining sides of the triangle KLM. If the lengths of the sides are a = 7 b = 5.6 c = 4.9 k = 5
