Area of Triangle Problems - page 20 of 42
Number of problems found: 837
- The sides
 The sides of the rectangle are in a ratio of 3:5, and its circumference measures 72 cm. Calculate: a) the size of both sides of the rectangle b) the area of the rectangle c) the length of the diagonals
The sides of the rectangle are in a ratio of 3:5, and its circumference measures 72 cm. Calculate: a) the size of both sides of the rectangle b) the area of the rectangle c) the length of the diagonals - Trapezoid thirds
 The ABCD trapezoid has parallel sides AB and CD. The E point lies on the AB side. The segment DE divides the trapezoid into two parts with the same area. Find the length of the AE line segment.
The ABCD trapezoid has parallel sides AB and CD. The E point lies on the AB side. The segment DE divides the trapezoid into two parts with the same area. Find the length of the AE line segment. - Recursion squares
 In the square, ABCD has inscribed a square so that its vertices lie at the centers of the sides of the square ABCD. The procedure of inscribing the square is repeated this way. The side length of the square ABCD is a = 20 cm. Calculate: a) the sum of peri
In the square, ABCD has inscribed a square so that its vertices lie at the centers of the sides of the square ABCD. The procedure of inscribing the square is repeated this way. The side length of the square ABCD is a = 20 cm. Calculate: a) the sum of peri - Centimeters 83177
 The carpenter cut a right-angled triangle with free sides of 550 mm and 200 mm from the wooden canvas, the face of a rectangle with dimensions of 80 CM and 65 CM. How many square centimeters will the waste make up?
The carpenter cut a right-angled triangle with free sides of 550 mm and 200 mm from the wooden canvas, the face of a rectangle with dimensions of 80 CM and 65 CM. How many square centimeters will the waste make up? - Perimeter of RT
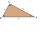 Find the circumference of the rectangular triangle if the sum of its legs is 22.5 cm and its area is 62.5 cm².
Find the circumference of the rectangular triangle if the sum of its legs is 22.5 cm and its area is 62.5 cm². - Right-angled 66364
 From a rectangular board with 2 m and 3 m dimensions, we cut isosceles and right-angled triangles at the corners with an overhang of 40 cm. Calculate the ratio of the rest of the board's areas to its total original area.
From a rectangular board with 2 m and 3 m dimensions, we cut isosceles and right-angled triangles at the corners with an overhang of 40 cm. Calculate the ratio of the rest of the board's areas to its total original area. - Calculate 8252
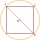 Calculate in cm² the area of a circle whose diameter is equal to the length of the diagonal of a square ABCD with a side of 4cm.
Calculate in cm² the area of a circle whose diameter is equal to the length of the diagonal of a square ABCD with a side of 4cm. - Decadal - flower bed
 The castle park includes a flower bed in the shape of a regular decagon with an area of 432.8 m². Determine the distance between the adjacent vertices of the flower bed.
The castle park includes a flower bed in the shape of a regular decagon with an area of 432.8 m². Determine the distance between the adjacent vertices of the flower bed. - Ratio in trapezium
 The ratio of the height v and the base a, c in the trapezoid ABCD is 1:6:3. Its area is 324 square cm, and the peak angle B is 35 degrees. Determine the perimeter of the trapezoid.
The ratio of the height v and the base a, c in the trapezoid ABCD is 1:6:3. Its area is 324 square cm, and the peak angle B is 35 degrees. Determine the perimeter of the trapezoid. - Railway embankment
 The railway embankment section is an isosceles trapezoid, and the bases' sizes are in the ratio of 5:3. The arms have a length of 5 m, and the embankment height is 4.8 m. Calculate the size of the embankment section area.
The railway embankment section is an isosceles trapezoid, and the bases' sizes are in the ratio of 5:3. The arms have a length of 5 m, and the embankment height is 4.8 m. Calculate the size of the embankment section area. - Horses playground
 The horse fence is a rectangular trapezoid with an area of 400 m². The base lengths should be 31 m and 19 m. If the boards are stacked in 5 rows, how many meters of fence will they need?
The horse fence is a rectangular trapezoid with an area of 400 m². The base lengths should be 31 m and 19 m. If the boards are stacked in 5 rows, how many meters of fence will they need? - Infinite sum of areas
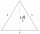 An equilateral triangle A1B1C1 is constructed above the height of the equilateral triangle ABC is constructed as. Above the height of the equilateral triangle A1B1C1 is built triangle A2B2C2, and so on. The procedure is repeated continuously. What is the
An equilateral triangle A1B1C1 is constructed above the height of the equilateral triangle ABC is constructed as. Above the height of the equilateral triangle A1B1C1 is built triangle A2B2C2, and so on. The procedure is repeated continuously. What is the - Diamond diagonals
 Find the diamond diagonal's lengths if the area is 156 cm² and the side is 13 cm long.
Find the diamond diagonal's lengths if the area is 156 cm² and the side is 13 cm long. - Czech flag
 Calculate the areas of the colored parts on Czech flag in the shape of a rectangle with dimensions of 2m and 1m. White and red form half the width, the blue triangle is isosceles, and its apex is half the length.
Calculate the areas of the colored parts on Czech flag in the shape of a rectangle with dimensions of 2m and 1m. White and red form half the width, the blue triangle is isosceles, and its apex is half the length. - Infinity
 A square with a side 19 long is an inscribed circle, and the circle is inscribed next to the square, circle, and so on to infinity. Calculate the sum of the area of all these squares.
A square with a side 19 long is an inscribed circle, and the circle is inscribed next to the square, circle, and so on to infinity. Calculate the sum of the area of all these squares. - RRL Basics
 What is the length of the smaller base of an isosceles trapezoid and the height, if a = 9 dm, the side is 6 dm and the angle ACB is 90 degrees?
What is the length of the smaller base of an isosceles trapezoid and the height, if a = 9 dm, the side is 6 dm and the angle ACB is 90 degrees? - Garden G
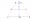 The rectangular, trapezoidal garden has a base length of 81m, 76m, and a vertical arm of 12m. Calculate how many m² of the area will remain for planting greenery if 1/3 of the area is built. Calculate the consumption of mesh for land fencing.
The rectangular, trapezoidal garden has a base length of 81m, 76m, and a vertical arm of 12m. Calculate how many m² of the area will remain for planting greenery if 1/3 of the area is built. Calculate the consumption of mesh for land fencing. - Free space in the garden
 The grandfather's free space in the garden was in the shape of a rectangular triangle of 5 meters and 12 meters in length. He decided to divide it into two parts and the height of the hypotenuse. The smaller part creates a rock garden, for the larger sows
The grandfather's free space in the garden was in the shape of a rectangular triangle of 5 meters and 12 meters in length. He decided to divide it into two parts and the height of the hypotenuse. The smaller part creates a rock garden, for the larger sows - Parallelogram - area
 Calculate the area of the parallelogram if the sides are a = 80, b = 60 long, and the size of the diagonal angle is 60°.
Calculate the area of the parallelogram if the sides are a = 80, b = 60 long, and the size of the diagonal angle is 60°. - 30-gon
 The radius of the inscribed circle is 15cm at a regular 30-gon. Find the side length a, circle radius R, circumference, and area.
The radius of the inscribed circle is 15cm at a regular 30-gon. Find the side length a, circle radius R, circumference, and area.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
