Unit conversion + triangle - practice problems
Number of problems found: 326
- A biker
 A biker traveled from city A to city B via city C with a uniform speed of 52 km/h. He then returned directly to city A with a uniform speed of 89 km/h. Find, in minutes, the total time of his whole journey to two decimal places. City distance A from B is
A biker traveled from city A to city B via city C with a uniform speed of 52 km/h. He then returned directly to city A with a uniform speed of 89 km/h. Find, in minutes, the total time of his whole journey to two decimal places. City distance A from B is - A triangular
 A triangular frame has sides that measure 15’-7",20’-4", and 26’-2". What is the total length of the three sides?
A triangular frame has sides that measure 15’-7",20’-4", and 26’-2". What is the total length of the three sides? - A radio antenna
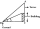 Avanti is trying to find the height of a radio antenna on the roof of a local building. She stands at a horizontal distance of 21 meters from the building. The angle of elevation from her eyes to the roof (point A) is 42°, and the angle of elevation from
Avanti is trying to find the height of a radio antenna on the roof of a local building. She stands at a horizontal distance of 21 meters from the building. The angle of elevation from her eyes to the roof (point A) is 42°, and the angle of elevation from - Three 235
 Three houses form a triangular shape. House A is 50 feet from house C and house B is 60 feet from house C. The measure is angle ABC is 80 degrees. Draw a picture and find the distance between A and B.
Three houses form a triangular shape. House A is 50 feet from house C and house B is 60 feet from house C. The measure is angle ABC is 80 degrees. Draw a picture and find the distance between A and B.
- Conjugate coordinates
 If the rectangular conjugate of the polar vector 12 angle 35 degrees is equal to x+yi, find the sum of x and y.
If the rectangular conjugate of the polar vector 12 angle 35 degrees is equal to x+yi, find the sum of x and y. - Subtract polar forms
 Solve the following 5.2∠58° - 1.6∠-40° and give answer in polar form
Solve the following 5.2∠58° - 1.6∠-40° and give answer in polar form - A lighthouse
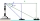 A lighthouse overlooks a bay, and it is 77 meters high. From the top, the lighthouse keeper can see a yacht southward at an angle of depression of 32 degrees and another boat eastward at an angle of 25 degrees. What is the distance between the boats?
A lighthouse overlooks a bay, and it is 77 meters high. From the top, the lighthouse keeper can see a yacht southward at an angle of depression of 32 degrees and another boat eastward at an angle of 25 degrees. What is the distance between the boats? - Piece of a wire
 A piece of wire is bent into the shape of a triangle. Two sides have lengths of 24 inches and 21 inches. The angle between these two sides is 55°. What is the length of the third side to the nearest hundredth of an inch? A: The length of the third side is
A piece of wire is bent into the shape of a triangle. Two sides have lengths of 24 inches and 21 inches. The angle between these two sides is 55°. What is the length of the third side to the nearest hundredth of an inch? A: The length of the third side is - A boy 5
 A boy starts at A and walks 3km east to B. He then walks 4km north to C. Find the bearing of C from A.
A boy starts at A and walks 3km east to B. He then walks 4km north to C. Find the bearing of C from A.
- A triangle 7
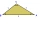 A triangle lot has the dimensions a=15m, b=10m, and c=20m. What is the measure of the angle between the sides of b and c?
A triangle lot has the dimensions a=15m, b=10m, and c=20m. What is the measure of the angle between the sides of b and c? - Using 4
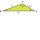 Using the law of cosines, find the measurement of leg b if the givens are B=20°, a=10, and c=15.
Using the law of cosines, find the measurement of leg b if the givens are B=20°, a=10, and c=15. - Rhombus 36
 Rhombus ABCD with side 8 cm long has diagonal BD 11.3 cm long. Find angle DAB.
Rhombus ABCD with side 8 cm long has diagonal BD 11.3 cm long. Find angle DAB. - One side 4
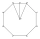 One side of a regular octagon is 12 inches. Find the apothem and its area.
One side of a regular octagon is 12 inches. Find the apothem and its area. - X-triangle
 Find the length of the x segment in the given triangle drawings.
Find the length of the x segment in the given triangle drawings.
- The apothem
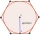 The apothem of a regular hexagon is 5√3 inches. Find one of its sides and area.
The apothem of a regular hexagon is 5√3 inches. Find one of its sides and area. - Gimli Glider
 Aircraft Boeing 767 lose both engines at 42000 feet. The plane captain maintains optimum gliding conditions. Every minute, lose 1910 feet and maintain constant speed 211 knots. Calculate how long it takes for a plane to hit the ground from engine failure.
Aircraft Boeing 767 lose both engines at 42000 feet. The plane captain maintains optimum gliding conditions. Every minute, lose 1910 feet and maintain constant speed 211 knots. Calculate how long it takes for a plane to hit the ground from engine failure. - Two aircraft
 Two planes fly to the airport. At some point, the first airplane is away from the airport by 98 km and the second 138 km. The first aircraft flies at an average speed of 420 km/h, and the second average speed is 360 km/h, while the tracks of both planes a
Two planes fly to the airport. At some point, the first airplane is away from the airport by 98 km and the second 138 km. The first aircraft flies at an average speed of 420 km/h, and the second average speed is 360 km/h, while the tracks of both planes a - Cross road
 From the junction of two streets perpendicular to each other, two cyclists (each on another street) walked out. One ran 18 km/h and the second 24 km/h. How are they away from a) 6 minutes, b) 15 minutes?
From the junction of two streets perpendicular to each other, two cyclists (each on another street) walked out. One ran 18 km/h and the second 24 km/h. How are they away from a) 6 minutes, b) 15 minutes? - Journey
 Charles and Eva stand in front of his house. Charles went to school south at a speed of 5.4 km/h, and Eva went to the store on a bicycle eastwards at 21.6 km/h. How far apart are they after 10 minutes?
Charles and Eva stand in front of his house. Charles went to school south at a speed of 5.4 km/h, and Eva went to the store on a bicycle eastwards at 21.6 km/h. How far apart are they after 10 minutes?
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
