Free space in the garden
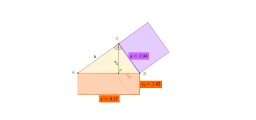
The grandfather's free space in the garden was in the shape of a rectangular triangle with 5 meters and 12 meters in length. He decided to divide it into two parts and the height of the hypotenuse. For the smaller part creates a rock garden, for the larger sows grass. How many square meters has a larger part?
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Enlarged 63034
Divide 130 nuts into two parts so that the smaller part enlarged 4 times equals the larger part reduced 3 times. How many nuts are in the smaller pile? - Gardens
The garden has the square shape with circumference 124 m. Divide it into two rectangular gardens, one should circumference 10 meters more than the second. What size will have a gardens? - Garden
The rectangular garden has dimensions of 27 m and 30 m. Peter and Katka split it in a ratio of 4:5. How many square meters did Katkin measure part of the garden? - Grandfather 47061
My grandfather made a fence around his rectangular garden measuring 7.2 meters and 12 meters. How many meters of mesh did he have to buy, and how much did he pay if one meter of mesh was € 5.90? - Thunderstorm
The height of the pole before the storm is 10 m. After a storm when they come to check it they see that on the ground from the pole blows part of the column. Distance from the pole is 3 meters. At how high was the pole broken? (In fact, a rectangular tria - Garden fence
The garden has the shape of a rectangular triangle with an area of 96 square meters and a 16 m long one leg. How many meters of the fence need to be fenced? - Grandfather's 7087
What height in meters is my grandfather's pool, if it can hold 7350 liters of water and the lower dimensions of the pool are 2.1 and 2.5 meters? - Grandfather's 5075
They have already produced 2,000 parts in their grandfather's workshop, five-sixths of the plan. How many components should they produce in total? - Grandfather's 3179
On a map with a scale of 1: 5000, the grandfather's garden is represented by a rectangle measuring 4 cm and 3 cm. What dimensions will it have on a map with a scale of 1: 4000? - Gardens
I have a garden in the shape of a square with a side length of 0.02 kilometers. Neighbor has a large garden as well and one side of the garden we share. I'd bought from a neighbor garden that my area of my garden increased to 5 ares. a/ By how many acres - Garden
The garden has a rectangular shape with lengths of 25 and 40 meters. It has been expanded so that each of its sizes increased by one-fifth. How many square meters increased its acreage? - Divide 44261
Divide the number 20 into two parts so that the first part is four times larger than the second. What is the ratio? - The tractor
The tractor sows an average of 1.5 ha per hour. In how many hours does it sows a rectangular trapezoid field with the bases of 635m and 554m and a longer arm 207m? - Rectangular 26091
The circular running track has a diameter of 130 meters. Is it possible to grass a rectangular surface with dimensions of 12m and 50m inside the circle? - Rectangular triangles
The lengths of corresponding sides of two rectangular triangles are in the ratio 2:5. At what ratio are medians relevant to hypotenuse these right triangles? At what ratio are the areas of these triangles? A smaller rectangular triangle has legs 6 and 8 c - Base of prism
The base of the perpendicular prism is a rectangular triangle whose legs length are at a 3: 4 ratio. The height of the prism is 2cm smaller than the larger base leg. Determine the volume of the prism if its surface is 468 cm². - Triangular prism
Calculate a triangular prism if it has a rectangular triangle base with a = 4cm and hypotenuse c = 50mm, and the height of the prism is 0.12 dm.
