Circle practice problems - page 36 of 50
Number of problems found: 990
- Nonagon
Calculate the area and perimeter of a regular nonagon if its radius of the inscribed circle is r = 10cm. - Axial section
The axial section of the cylinder has a diagonal 50 cm. The shell size and base surface are in the ratio 2:5. Calculate the volume and surface area of this cylinder. - Hexagon in circle
Calculate the radius of a circle whose length is 10 cm greater than the circumference of a regular hexagon inscribed in this circle. - Triangle
In triangle ABC, there is a point S with the center of the inscribed circle. The area of quadrilateral ABCS is equal to four-fifths of the area of triangle ABC. The lengths of the sides of triangle ABC expressed in centimeters are all integers and the - The Indian tent
The Indian tent is cone-shaped. Its height is 3.5 m. The diameter of the base is 2.5 m. How much canvas is needed to make a tire? - Steel tube
The steel tube has an inner diameter of 4 cm and an outer diameter of 4.8 cm. The density of the steel is 7800 kg/m³. Calculate its length if it weighs 15 kg. - Concentric 18343
Construct three concentric circles k, l, m with center at point S and with radii 2cm, 3cm, and 40mm - Again saw
We have a sculpture beam from the tree trunk with a rectangular cross-section with dimensions 91 mm and 87 mm. What is the trunk's smallest diameter? - Rectangle
The rectangle is 21 cm long and 38 cm wide. Find the radius of the circle circumscribing the rectangle. - Spherical cap 4
What is the surface area of a spherical cap, the base diameter of 20 m, and the height of 2.5 m? Calculate using the formula. - Slant height
Find the cone's volume. The cone's slant height is 5cm, and the radius of its base is 3cm. - Intersect 6042
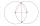Two circles with straight radii of 58 mm intersect at two points. Their common string is 80 mm long. What is the distance of the centers of these circles? - Conditions 7186
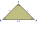Given an isosceles right triangle ABS with base AB. On a circle centered at point S and passing through points A and B, point C lies such that triangle ABC is isosceles. Determine how many points C satisfy the given conditions and construct all such point - Determine 12331
An annulus with an area S = 4.2 square meters has an inner radius r = 2.25 m. Determine the outer radius of the annulus. - Hypotenuse 78844
Construct triangle KLM if side m=6.5cm, hypotenuse tm=4cm, height to side m: vm=3.2cm - The length
The length of the circle is 24 cm. What is the circular arc length of the corresponding angle of 30°? - Circumscribed circle ABC
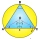Triangle ABC, with sides a = 15 cm, b = 17.4 cm, and c = 21.6 cm, is circumscribed by a circle. Calculate the area of the segments determined by the sides of the triangle. - Circular railway
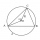The railway connects points A, B, and C in a circular arc, whose distances are | AB | = 30 km, AC = 95 km, and BC | = 70 km. How long will the track be from A to C? - Circumscribed 2671
The circle's radius circumscribed by the rectangle is 5 cm, and one side of the rectangle is 6 cm long. Calculate the length of the other side and the area of the rectangle. - Inscribed 43991
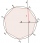An irregular convex octagon is inscribed in the circle. Its four adjacent sides have a length of 3, and the remaining four adjacent sides have a size of 2. What is the area of a given octagon?
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
