Equations practice problems - page 42 of 241
Number of problems found: 4806
- Complementary 81152
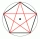In a certain polygon, the ratio of the sum of the sizes of its internal angles and the sum of the sizes of the complementary angles is 2:5. How many vertices does this polygon have? - Together 81151
Matěj has 2 more marbles than three times the number of marbles that Lojza. Both together have 18 balls. How many marbles does Lojza have? - Father 81149
The father is older than the son by the ratio of 5:2. Dad is older than 33. How old are they both? - Bigger 81145
In 10 years, the teddy bear will be three times bigger than it is today. How old is the teddy bear now? - Quatrefoil 81138
Gothic quatrefoil is an ornament in which four identical touching smaller circles are inscribed in a larger circle, as you can see in the picture. The radius of the great circle is one meter. Calculate the radius of the smaller circle in meters. - Quadrilateral and angles
In a quadrilateral, angle α is twice as large as angle β. Angle γ is 80% of angle α, and angle δ is 30° greater than angle α. Determine the angles of this quadrilateral. - Percentage - fence
We are painting a wooden fence. On the first day, we painted one-half of the fence. The next day, we painted half of the remaining part. On the third day, again, half of the remaining part. After the third painting, we had 12.5 meters of unpainted fence l - Classification 81133
One of the conditions for classification with grade 2 in geography is to obtain an average of at least 64 points from four tests. The minimum number of points a skater must receive from the fourth test to meet this condition is if she received 59, 67, or - Introduced 81104
The * (asterisk) operation assigning one number to two pairs of numbers is introduced as follows: (a, b)*(c, d) = ac+bd We know that: (x,2)*(-1, v) = -1 and (2,-1)*(u, v)=5 and (u, v)*(1,1)=-2 What is (1,2)*(x, y) equal to if y=3? - Chocolate 81103
I paid 36 crowns for butter and chocolate. Butter was CZK 6 more expensive than chocolate. How much did the chocolate cost? - Painters 81101
Four painters painted the house in 14 days. How long will it take if 2 more come to help after 5 days? - Dimensions 81100
The area of the rectangle is 81.25 cm². If we increase its length by 5 mm, its area increases by 4%. Determine its dimensions. - Unknown 81081
The number 420 is 20% more than the unknown number. What is the unknown number? - Numbers 81079 The ratio of the two numbers is 1:3. Half of the larger one is 135. What is the sum of the two numbers?
- Circle and chord
The chord of a circle is 233 long, and the length of the circular arc above the chord is 235. What is the circle's radius, and what is the central angle of the circular arc? - Part-time 81067 I had 350 euros left over from the money I earned from the part-time job. I bought soccer cleats with half of the money I earned and a soccer ball with the other half. How much did I earn from the part-time job?
- Three-digit - sum A three-digit number has a digit sum of 16. If we change the digits in the hundreds and tens places in this number, the number is reduced by 360. If we swap the ten's and one's digits in the original number, the number increases by 54. Find this three-dig
- Participants 81059
Participants paid out 3,300 euros in 40 banknotes. Some were 50e, and others were 100e. How many were there? - Cleaners 81056
Four cleaners will clean the hotel in 15 hours. How long will they clean if, after 8 hours, one gets injured and leaves? - Younger Carlos In 2005, Peter was three times as old as Carlos. In 2020, Carlos was half his age younger than Peter. In which year was Peter born and in which Carlos?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
