Grade - math word problems - page 239 of 950
Number of problems found: 18986
- A biologist
 A biologist knows that the average length of a leaf of a certain plant is 4 inches. The standard deviation of the population is 0.6 inches. A sample of 20 leaves of that type of plant given a new type of plant food had an average length of 4.2 inches. At
A biologist knows that the average length of a leaf of a certain plant is 4 inches. The standard deviation of the population is 0.6 inches. A sample of 20 leaves of that type of plant given a new type of plant food had an average length of 4.2 inches. At - Swimming pool 6
 We open the first pipe and, after two hours, open the second pipe without closing the first. The swimming pool will be filled with both pipes in four hours. If we open the first pipe itself, it will fill the pool 1.5 times faster than the second pipe. How
We open the first pipe and, after two hours, open the second pipe without closing the first. The swimming pool will be filled with both pipes in four hours. If we open the first pipe itself, it will fill the pool 1.5 times faster than the second pipe. How - A hiker
 A hiker plans to hike up one side of a mountain and down the other side of points a mountain, each side of the mountain formed by a straight line. The angle of elevation at the starting point is 42.4 degrees, and the angle of elevation at the end is 48.3
A hiker plans to hike up one side of a mountain and down the other side of points a mountain, each side of the mountain formed by a straight line. The angle of elevation at the starting point is 42.4 degrees, and the angle of elevation at the end is 48.3 - Groups 72194
 I have eight groups. How could they place first, second, and third?
I have eight groups. How could they place first, second, and third? - Three-digit 72184
 How many three-digit numbers can be created from the numbers 1, 2, 3, and 4 if you can repeat them?
How many three-digit numbers can be created from the numbers 1, 2, 3, and 4 if you can repeat them? - Balloons 72174
 On the first day, 25% of the balloons were sold. On the second day, 45% of the balloons were. How many percents of balloons did they have left on the third day?
On the first day, 25% of the balloons were sold. On the second day, 45% of the balloons were. How many percents of balloons did they have left on the third day? - A rectangle 10
 A rectangle has a length of 8 millimeters and an area of 216 square millimeters. What is the width? What is the perimeter?
A rectangle has a length of 8 millimeters and an area of 216 square millimeters. What is the width? What is the perimeter? - Chocolates 72154
 Adam and Andrej bought sweets. Adam paid € 2.9 for three chocolates and 2 bars, and Andrej paid € 4 for four chocolates and 3 bars. How much did the chocolate cost, and how much did the bar cost?
Adam and Andrej bought sweets. Adam paid € 2.9 for three chocolates and 2 bars, and Andrej paid € 4 for four chocolates and 3 bars. How much did the chocolate cost, and how much did the bar cost? - 150 percent
 One hundred fifty percent of what number is 15? 150% of x is 15.
One hundred fifty percent of what number is 15? 150% of x is 15. - Centimeters 72134
 The area of the square is equal to 1024 square centimeters. Calculate the perimeter of the square and the length of the side a.
The area of the square is equal to 1024 square centimeters. Calculate the perimeter of the square and the length of the side a. - Number 72124
 The ratio of three times the number x and twice the number 9 equals 3. What is the value of the number x?
The ratio of three times the number x and twice the number 9 equals 3. What is the value of the number x? - The temperature 32
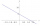 The temperature in a place in Antarctica at noon is 5°Celsius, and every hour, it drops 4 °Celsius. Express this relationship using one equation and represent it graphically.
The temperature in a place in Antarctica at noon is 5°Celsius, and every hour, it drops 4 °Celsius. Express this relationship using one equation and represent it graphically. - Temperature 72104
 Jaroslav had a temperature of 36.8 °C in the morning. In the afternoon, it had a temperature of 38.4 °C. How many °C did Jaroslav's temperature rise?
Jaroslav had a temperature of 36.8 °C in the morning. In the afternoon, it had a temperature of 38.4 °C. How many °C did Jaroslav's temperature rise? - Cylinder 72094
 The tank has the shape of a rotating cylinder with a base radius of 6 m reach. Water flows at a speed of 2 liters per second for 3 hours. To what height does the water in the tank?
The tank has the shape of a rotating cylinder with a base radius of 6 m reach. Water flows at a speed of 2 liters per second for 3 hours. To what height does the water in the tank? - František 72084
 Peter and František are 102 years old. František is 12 years younger than Petr. How old is Peter?
Peter and František are 102 years old. František is 12 years younger than Petr. How old is Peter? - Pancake mix
 According to a recipe, each batch of pancake mix can make 12 pancakes. Lilly is making three batches for a brunch party. If each batch needs 7/12 cups of milk, how much milk does she need in total?
According to a recipe, each batch of pancake mix can make 12 pancakes. Lilly is making three batches for a brunch party. If each batch needs 7/12 cups of milk, how much milk does she need in total? - The largest 4
 The largest room in the quarantine area is 45 m long and 30 m wide. The height of the room is 15 m. If the occupancy guidelines recommend at least five m³ per person, what is the maximum number of people allowed in the room?
The largest room in the quarantine area is 45 m long and 30 m wide. The height of the room is 15 m. If the occupancy guidelines recommend at least five m³ per person, what is the maximum number of people allowed in the room? - Number 72054
 I think the number. Its value equals the sum of three times the number 12 and the number 9. What number do I think?
I think the number. Its value equals the sum of three times the number 12 and the number 9. What number do I think? - Parallelogram 72044
 Assembly parallelogram ABCD: AB = 4.8cm, va = 3cm, BC = 4cm. Calculate the circuit. Make a sketch.
Assembly parallelogram ABCD: AB = 4.8cm, va = 3cm, BC = 4cm. Calculate the circuit. Make a sketch. - Bedroom floor
 Jayson's square bedroom floor measures 2m on its side. How big should the carpet be to cover the whole floor?
Jayson's square bedroom floor measures 2m on its side. How big should the carpet be to cover the whole floor?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
