Grade - math word problems - page 499 of 950
Number of problems found: 18986
- The surface area
How much percent will the surface area of a 4x5x8 cm block increase if the length of the shortest edge is increased by 2 cm? - Concentric 18343
Construct three concentric circles k, l, m with center at point S and with radii 2cm, 3cm, and 40mm - Rectangular 18333
The rectangular pool has dimensions of 10.5m and 8m. There is a 1m wide trail around it. How many m² of tiles are needed to pave the sidewalk? - Destination 18323
The family went on a trip to a ruin 6 km away. The father had a step length of 0.75 m, the mother of 0.6 m, and little Eva 50 cm. They went out on the same step. How many times did their steps retrace before reaching their destination? - Trapezoid 18313
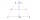Find the points A1 B1 symmetric along the y-axis to the points A [-4,0] and B [-1,4]. Calculate the perimeter of the trapezoid AB B1 A1. - Cylinder-shaped 18303
How much water is in a cylinder-shaped pool with a radius of 2m, which is 1.5 m deep if it is filled 10 cm below the edge rounded to one decimal place - Container 18293
I poured ten full cups with a radius of 5 cm and a height of 10 cm into a container with a volume of 8 liters. How many liters are in the container? - Cylinder-shaped 18283 How much fabric will be needed to cover a cylinder-shaped seat with a diameter of 0.8 m, 0.6 m high (rounded up to whole square meters)
- Diameter 18273
The roller on the tennis court has a diameter of 60 cm and is 1.2 m wide. What area will the roller cover in one turn? They rounded to one decimal place. - Half-height 18253
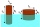The cylinder has a volume of 200 liters. What is the volume in liters of a second cylinder twice as wide and half-height? (π = 3.14) - Correctly 18243
Pupils have 10 points for each correctly solved task. They will be deducted 5 points for the wrong solution. After solving 20 tasks, Marian had 80 points. How many tasks did he solve correctly, and how many did not? - Equation - words
Determine the unknown number for which it applies: whose four times increased by the number 3 equals its double. - Sine theorem 2
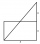From the sine theorem, find the ratio of the sides of a triangle whose angles are 30°, 60°, and 90°. - Produced 18213
In the factory, they produced 1,500 products a week on five machines. How many machines do they need to produce 2,000 products a week? - Original 18203
There is a cube with an edge. How long must the cube's edge be in which the volume should be twice the volume of the original cube? - Vector equation
Let's v = (1, 2, 1), u = (0, -1, 3) and w = (1, 0, 7). Solve the vector equation c1 v + c2 u + c3 w = 0 for variables c1, c2, c3 and decide whether v, u, and w are linear dependent or independent - Cardboard box
Peter had square cardboard. The length of the edges was an integer in decimetres. He cut four squares with a side of 3 dm from the corners and made a box out of it, which fit precisely 108 cubes with an edge one dm long. Julia cut four squares with a side - Classmates 18173
Classmates Anka, Bea, Villa, and Danka can sit next to each other on the bus. What and how many ways can they sit down? - Nutballs
The dough for nutballs contains, among other things, two basic raw materials: flour and nuts, in a ratio of 2:1. How much flour is needed, and how many nuts are needed for 1 kg of dough if the "other" is 100g? - Ducats
The king divided the ducats into his three sons in a ratio of 2:5:4. How many ducats did the king divide them if the youngest received 260 ducats, the least of all sons?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
