Examples for secondary school students - page 3 of 231
Number of problems found: 4610
- Four numbers 3
 What least number must be added to each of the numbers 6,15,20 and 43 to make them proportional?
What least number must be added to each of the numbers 6,15,20 and 43 to make them proportional? - The angle 9
 The angle of elevation of the top of a tower from a point A on the ground is 30°. On moving a distance of 20 m towards the foot of the tower to a point B, the angle of elevation increases to 60°. Find the height of the tower and the distance of the tower
The angle of elevation of the top of a tower from a point A on the ground is 30°. On moving a distance of 20 m towards the foot of the tower to a point B, the angle of elevation increases to 60°. Find the height of the tower and the distance of the tower - GP - terms
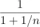 Which term of the G.P., 2, 8, 32, ... up to n terms is 131072?
Which term of the G.P., 2, 8, 32, ... up to n terms is 131072? - Triple the sum
 At what rate a sum triples in 5 years at simple interest?
At what rate a sum triples in 5 years at simple interest? - Triangle 90
 Triangle made by 6 cm 4.5 cm and 7.5 cm. what angles does it make?
Triangle made by 6 cm 4.5 cm and 7.5 cm. what angles does it make? - The sum 51
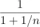 The sum of two numbers is 100 and difference is 37 . Find the difference between their squares.
The sum of two numbers is 100 and difference is 37 . Find the difference between their squares. - Percents and ratio
 When 20% of a number is added to another number, the number increases by 50%. What is the ratio of the two numbers?
When 20% of a number is added to another number, the number increases by 50%. What is the ratio of the two numbers? - Reciprocal in equation
 A positive number, when increased by 10 equals 200 times its reciprocal. What is the number?
A positive number, when increased by 10 equals 200 times its reciprocal. What is the number? - The boat
 A boatman goes 2 km against the stream in 40 minutes and returns to the same spot in 30 minutes. What is his rate of rowing in still water?
A boatman goes 2 km against the stream in 40 minutes and returns to the same spot in 30 minutes. What is his rate of rowing in still water? - A plane 3
 A plane left 30 minutes later than the scheduled time and in order to reach the destination 1500 km away in time, it has to increase the speed by 250 km/hr from the usual speed. Find its usual speed.
A plane left 30 minutes later than the scheduled time and in order to reach the destination 1500 km away in time, it has to increase the speed by 250 km/hr from the usual speed. Find its usual speed. - Dual profit
 A merchant has 1000 kg of sugar, part of which he sells at 8% profit and the rest 18%. He gains 14% on the whole. Find the quantity of 8% profit.
A merchant has 1000 kg of sugar, part of which he sells at 8% profit and the rest 18%. He gains 14% on the whole. Find the quantity of 8% profit. - Dilution
 How many liters of water will have to be added to 1125 liters of the 45% solution of acid so that the resulting mixture will contain more than 25% but less than 30% acid content?
How many liters of water will have to be added to 1125 liters of the 45% solution of acid so that the resulting mixture will contain more than 25% but less than 30% acid content? - Three inscribed objects
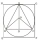 A circle is inscribed in a square. An equilateral triangle of side 4√3 is inscribed in that circle. Find the length of the diagonal of the square.
A circle is inscribed in a square. An equilateral triangle of side 4√3 is inscribed in that circle. Find the length of the diagonal of the square. - Lightbulbs
 The physical plant at the main campus of a large state university recieves daily requests to replace fluorescent lightbulbs. The distribution of the number of daily requests is bell-shaped and has a mean of 48 and a standard deviation of 10. Using the emp
The physical plant at the main campus of a large state university recieves daily requests to replace fluorescent lightbulbs. The distribution of the number of daily requests is bell-shaped and has a mean of 48 and a standard deviation of 10. Using the emp - Two trains 16
 Two trains cross each other in 14 seconds when they are moving in opposite direction and when they are moving in the same direction they cross each other in 3 minutes 2 seconds . The speed of the faster train is by what percent more than the slower train?
Two trains cross each other in 14 seconds when they are moving in opposite direction and when they are moving in the same direction they cross each other in 3 minutes 2 seconds . The speed of the faster train is by what percent more than the slower train? - Failed in examination
 In an examination, 20% of total students failed in history,15% failed in English and 5% of total number of students failed in both subjects. Find the percentage of total number of students who passed in both the subjects.
In an examination, 20% of total students failed in history,15% failed in English and 5% of total number of students failed in both subjects. Find the percentage of total number of students who passed in both the subjects. - Usual speed 2
 A passenger train takes 1 h less for a journey of 120 km.If its speed increased by 10 k/h from its usual speed. What is its usual speed?
A passenger train takes 1 h less for a journey of 120 km.If its speed increased by 10 k/h from its usual speed. What is its usual speed? - Angle of elevation
 From a point A on the ground, the angle of elevation of the top of a 20 m tall of a building is 45°. A flag is hoisted at the top of the building and the angle of elevation of the top of the flagstaff from A is 60°. Find the length of the flagstaff and th
From a point A on the ground, the angle of elevation of the top of a 20 m tall of a building is 45°. A flag is hoisted at the top of the building and the angle of elevation of the top of the flagstaff from A is 60°. Find the length of the flagstaff and th - A furniture
 A furniture dealer bought a dining set at 12000 USD. At what price would the dealer sell this set by offering a discount of 5% and still make a profit of 10%?
A furniture dealer bought a dining set at 12000 USD. At what price would the dealer sell this set by offering a discount of 5% and still make a profit of 10%? - A variable
 A variable rectangle has a constant area of 35 cm². Find the lengths of the sides when the perimeter is minimum.
A variable rectangle has a constant area of 35 cm². Find the lengths of the sides when the perimeter is minimum.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
