Examples for secondary school students - page 31 of 231
Number of problems found: 4608
- Three-digit - sum
 A three-digit number has a digit sum of 16. If we change the digits in the hundreds and tens places in this number, the number is reduced by 360. If we swap the ten's and one's digits in the original number, the number increases by 54. Find this three-dig
A three-digit number has a digit sum of 16. If we change the digits in the hundreds and tens places in this number, the number is reduced by 360. If we swap the ten's and one's digits in the original number, the number increases by 54. Find this three-dig - Distribution 81063
 The weight of a loaf of bread should be 900 g. Loaves whose weight differs by more than 30 g from this value must be rejected. Determine the probability that a loaf is rejected if its weight has a normal distribution N(900,40).
The weight of a loaf of bread should be 900 g. Loaves whose weight differs by more than 30 g from this value must be rejected. Determine the probability that a loaf is rejected if its weight has a normal distribution N(900,40). - Individual 81044
 CZK 895 was paid for three ties. A blue tie was 18% more expensive than a gray one, and a brown one was CZK 100 more expensive than a gray one. Calculate the prices of individual ties.
CZK 895 was paid for three ties. A blue tie was 18% more expensive than a gray one, and a brown one was CZK 100 more expensive than a gray one. Calculate the prices of individual ties. - Quadrilateral 81033
 The foundations of a regular truncated quadrilateral pyramid are squares. The lengths of the sides differ by 6 dm. Body height is 7 dm. The body volume is 1813 dm³. Calculate the lengths of the edges of both bases.
The foundations of a regular truncated quadrilateral pyramid are squares. The lengths of the sides differ by 6 dm. Body height is 7 dm. The body volume is 1813 dm³. Calculate the lengths of the edges of both bases. - Thanks 81022
 Pavla is 2x older than Irena. Four years ago, Pavla was 6 times older than Irena was then. In how many years will the ages of Pavla and Irena be in the ratio of 4:3? Thanks
Pavla is 2x older than Irena. Four years ago, Pavla was 6 times older than Irena was then. In how many years will the ages of Pavla and Irena be in the ratio of 4:3? Thanks - Triangle 80994
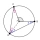 In the triangle, ABC, the angles alpha and beta axes subtend the angle phi = R + gamma/2. R is a right angle of 90°. Verify.
In the triangle, ABC, the angles alpha and beta axes subtend the angle phi = R + gamma/2. R is a right angle of 90°. Verify. - Cross-sectional 80979
 An undisciplined motorcyclist drove at an unreasonable speed on a mountain road, lost control in a bend, and left the roadway at 90 km/h. He was falling into a gully 36 m deep. Draw a cross-sectional picture of the whole situation. How far did the motorcy
An undisciplined motorcyclist drove at an unreasonable speed on a mountain road, lost control in a bend, and left the roadway at 90 km/h. He was falling into a gully 36 m deep. Draw a cross-sectional picture of the whole situation. How far did the motorcy - Agricultural
 Last year, the Agro agricultural company sowed wheat on land with a total area of 29 ha and rye on land with a total area of 18 ha. From all these lands, it harvested a total of 137.4 tons of grain. The sum of the average yields per hectare of wheat a
Last year, the Agro agricultural company sowed wheat on land with a total area of 29 ha and rye on land with a total area of 18 ha. From all these lands, it harvested a total of 137.4 tons of grain. The sum of the average yields per hectare of wheat a - Participants 80965
 After the meeting, all participants shook hands with each other - a total of 105 times. How many people were there at the meeting?
After the meeting, all participants shook hands with each other - a total of 105 times. How many people were there at the meeting? - Five-minute 80951
 Karel has an average grade of exactly 1.12 from five-minute episodes. Prove that at least 22 of them have one.
Karel has an average grade of exactly 1.12 from five-minute episodes. Prove that at least 22 of them have one. - Probability - test
 The test contains 11 questions, each question has 4 options (only one correct). Find the probability that less than 2 questions will be answered correctly. (The probability of a correctly answered question is 1/4.) (Write the result as a whole number in p
The test contains 11 questions, each question has 4 options (only one correct). Find the probability that less than 2 questions will be answered correctly. (The probability of a correctly answered question is 1/4.) (Write the result as a whole number in p - Elevation of the tower
 We can see the top of the tower standing on a plane from a certain point A at an elevation angle of 39°25''. If we come towards its foot 50m closer to place B, we can see the top of the tower from it at an elevation angle of 56°42''. How tall is the tower
We can see the top of the tower standing on a plane from a certain point A at an elevation angle of 39°25''. If we come towards its foot 50m closer to place B, we can see the top of the tower from it at an elevation angle of 56°42''. How tall is the tower - Elevation 80866
 Find the height of the tower when the geodetic measured two angles of elevation α=34° 30'' and β=41°. The distance between places AB is 14 meters.
Find the height of the tower when the geodetic measured two angles of elevation α=34° 30'' and β=41°. The distance between places AB is 14 meters. - Probability 80860
 During the exam, the student takes 3 questions out of 20. He is ready for 14 of them. Find the probability that he draws at least one that he knows.
During the exam, the student takes 3 questions out of 20. He is ready for 14 of them. Find the probability that he draws at least one that he knows. - Centimeters 80859
 Triangle ABC and triangle ADE are similar. Calculate in square centimeters the area of triangle ABC if the length of side DE is 12 cm, the length of side BC is 16 cm, and the area of triangle ADE is 27 cm².
Triangle ABC and triangle ADE are similar. Calculate in square centimeters the area of triangle ABC if the length of side DE is 12 cm, the length of side BC is 16 cm, and the area of triangle ADE is 27 cm². - Probability 80858
 During the exam, the student takes 3 questions out of 30. He is ready for 20 of them. Find the probability that he draws at most 2 that he knows.
During the exam, the student takes 3 questions out of 30. He is ready for 20 of them. Find the probability that he draws at most 2 that he knows. - Probability 80857
 During the exam, the student answers 4 questions out of 25. He is ready for 20 of them. Find the probability that he draws exactly one that he does not know.
During the exam, the student answers 4 questions out of 25. He is ready for 20 of them. Find the probability that he draws exactly one that he does not know. - Probability 80856
 The probability of occurrence of a certain phenomenon is the same in all trials and is equal to 0.7. Attempts are repeated until this phenomenon occurs. What is the probability that we will have to make a fifth trial?
The probability of occurrence of a certain phenomenon is the same in all trials and is equal to 0.7. Attempts are repeated until this phenomenon occurs. What is the probability that we will have to make a fifth trial? - Probability - coin toss
 A coin is tossed 24 times. Find the probability of getting 16 heads. (The probability of getting a head is 0.5)
A coin is tossed 24 times. Find the probability of getting 16 heads. (The probability of getting a head is 0.5) - Longitudinal 80822
 How does the rail lengthen when the temperature changes from -30°C to 30°C if it is 25 m long at 0°C? The temperature coefficient of longitudinal expansion is 12.10na-6Kna-1.
How does the rail lengthen when the temperature changes from -30°C to 30°C if it is 25 m long at 0°C? The temperature coefficient of longitudinal expansion is 12.10na-6Kna-1.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
