Isolating a variable in the formula - practice problems - page 4 of 144
Number of problems found: 2863
- Two trains 11
Two trains running in opposite direction cross a man standing on the platform in 27 seconds and 17 seconds and they cross each other in 23 seconds. Find the ratio of their speeds. - The speeds
The speeds of three cars are in the ratio 2:3:4. What is the ratio of the times taken by these cars to travel the same distance? - One combine
One combine harvester can harvest a field of corn in 4.5 hours. Another harvester can harvest the same field in 3 hrs. If the farmer uses the two harvesters at the same time. How long will it take to harvest the entire field? - A tank 2
A tank can be filled by a pipe A in 3 hours and by pipe B in 5 hours. When the tank is full, it can be drained by pipe C in 4 hours. If the tank is initially empty and all three pipes are open, how many hours will it take to fill up the tank?
- Consumption stable
If the price of sugar rises from Rs 6/kg to Rs 7.50/kg. A person having no increase in his expenditure on sugar, will have to reduce his consumption by? - Negative term
Which term of the AP 24,21,18,15,.....is the first negative term? - The average 15
The average age of a group of four men whose ages are in the ratio of 2:3:4:5 is 42 years, what is the age of the eldest person of this group? - Three Numbers GP
The sum of three Numbers in geometric progression (GP) is 38, and their product is 1728. Find the Numbers. - A man 21
A man sells a bicycle at a profit of 25%. Had he bought it at a price less by 25% and sold it at 250 euro less then also he could have made a profit of 25%. Find cost price.
- Height or altitude
Find the altitude (in cm) of side MT of triangle MNT with side MN = 36 cm, MT = 36 cm and NT = 48 cm. - Parallel sides
Area of trapezium is 45 sq cm and sum of the length of parallel sides is 15 cm. Find height of the trapezium. - Three ratios 2
What is the ratio of bases of two triangles when the ratio of their heights is 3:4 and the ratio of their areas is 4:3? - PQR - Euclid
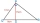Find the length of line segment PR - leg of the right triangle PQR. PQ=17 cm PS=15 cm QS=8 cm; Point S is the height touch point with a hypotenuse of the RQ. - A conical
A conical tent can accommodate 11 people. Each person needs 4 m² of space on the ground and 20 m³ of air to breathe. Find the height of the tent.
- Melting 3 cubes
The sides of the three metal cubes are 30 cm, 40 cm, and 50 cm, respectively. Find the side of the new cube formed by melting these cubes together. - Two numbers at a ratio
If 1.5x = 0.04y, then find the value of {(y - x)/(y + x)}. - Three workers
A can do a work in 16 hours, and B alone in 24 hours. If A, B, and C work together and finish it in 8 hours, then C alone can finish it in how many hours? - A rectangle 14
A rectangle is 8 cm long and 5 cm wide. Its perimeter is doubled when each of its sides is increased by x cm. From an equation in x, find the new length of the rectangle. - A,B,C,D
A, B, C, D are four consecutive odd integers and their average is 42. What is the product of B and D?
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
