Line - math word problems - page 12 of 29
Number of problems found: 574
- Parametric equation
Point A [6; -2]. Point B = [-3; 1] Write the parametric equation of the line BA so that t belongs to the closed interval < 0;3 > - Half-planes 36831
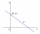The line p and the two inner points of one of the half-planes determined by the line p are given. Find point X on the line p so that the sum of its distances from points A and B is the smallest. - The midpoint The midpoint of (2, 5) and (8, y) is (5, -1). Find the line equation in slope-intercept form.
- Inner angles
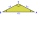The magnitude of the internal angle at the central vertex C of the isosceles triangle ABC is 72°. The line p, parallel to the base of this triangle, divides the triangle into a trapezoid and a smaller triangle. How big are the inner angles of the trapezoi - Interpretation 35461
The arranger should line up two identical white sweaters, two identical green sweaters, and one blue sweater in the shop window. How many possible ways can the interpretation be adjusted? - Line segment
Line segment AB is 8 cm long. Divide it by a ratio of 2:3. - Temperature 34641
The aluminum line has a resistance of 7.6Ω at -10˚C. What will be its resistance at a temperature of + 50˚C?
- Four-sevenths 34451
In how many parts do I have to divide the line whose endpoints are the images of the numbers 0 and 1 on the number axis so that they can be displayed: three-fifths, four-sevenths, five-eighths, and six-sixths - Double-track line
A 160 m long passenger train runs on a double-track line in one direction at a constant speed of 54 km/h, and a 240 m long express train in the opposite direction. a) How fast is the express train if passing the passenger train driver for 6 s? b) How long - Three roads
The three boys moved from start to finish on three different routes, A, B, and C, always simultaneously. Adam drove road A 1500 m long on a scooter. Blake walked route B 600 m long on foot. Cyril got on a scooter on route C after a 90 m walk, then he left - Acute triangle
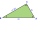In the acute triangle KLM, V is the intersection of its heights, and X is the heel of height to the side KL. The axis of the angle XVL is parallel to the side LM, and the angle MKL is 70°. What size are the KLM and KML angles? - Perpendicular projection Determine the distance of point B[1, -3] from the perpendicular projection of point A[3, -2] on a straight line 2 x + y + 1 = 0.
- Direction vector The line p is given by the point P [- 0,5; 1] and the direction vector s = (1,5; - 3) determines: A) value of parameter t for points X [- 1,5; 3], Y [1; - 2] lines p B) whether the points R [0,5; - 1], S [1,5; 3] lie on the line p C) parametric equations
- Nautical miles
How many nautical miles do they sail if the route is shown on a 1:25 000 scale map with a 7.4 cm long line? - Place vector
Place the vector AB if A (3, -1), B (5,3) in point C (1,3) so that AB = CO.
- Reduction 33021
Draw the line AB = 14 cm and divide it by the reduction angle in the ratio of 2:9. - Construction 32971
There is any circle k that does not have a marked center. Use a suitable construction to find the center of the circle k. Try on two different circles. - Ascend vs. descent Which function is growing? a) y = 2-x b) y = 20 c) y = (x + 2). (-5) d) y = x-2
- Represents 32931
Jeníček will go on vacation with his parents and go by boat for a certain part of the journey. He is interested in how many nautical miles they will sail if their route represents by a line 7.4 cm long on a 1:25,000 scale map. (1 nautical mile = 1,850 m) - Proportion 32223
Compare line lengths by ratio and proportion. a) AB = 2 cm, | KL | = 8 cm (b) | EF | = 28 cm, | MN | = 21 cm
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
