Minimum - practice problems
The minimum is the smallest value in a set of numbers or the lowest point on a function within a specified domain. In calculus, local minima occur where a function changes from decreasing to increasing, found by setting the derivative to zero and applying the second derivative test. Global minima represent the absolute lowest value across the entire domain. Minimum problems are essential in optimization, seeking to find the least amount of resources, time, or cost needed. Real-world applications include minimizing material usage, reducing travel distance, and finding optimal production levels. Identifying minima requires understanding of functions, critical points, and inequality constraints.Directions: Solve each problem carefully. Show all your work.
Number of problems found: 110
- A person 3
A person distributes his pens among four friends A, B, C and D in the ratio 1/3 : 1/4 : 1/5 : 1/6. What is the minimum number of pens that the person should have? - A variable
A variable rectangle has a constant area of 35 cm². Find the lengths of the sides when the perimeter is minimum. - Minimum interior angle
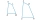What is the minimum interior angle possible for a regular polygon? - The size 3
The size of a wooden block is 15cm × 12cm × 20cm. How many such blocks will be required to construct a solid wooden cube of minimum size? - Amy needs
Amy needs to serve 100 people with hashed browns. The hashed browns are sold in packs of 8 boxes, and each box in the pack serves 4 people. How many packs should she buy, minimum? How many people will she be able to serve with this purchase? - Tent - spherical cap
I have a tent in the shape of a spherical cap. Assume we want the volume to be 4 cubic meters, to sleep two or three people. Assume that the material making up the dome of the ten is twice as expensive per square as the material touching the ground. What - Min-max
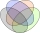What is the maximum and minimum of the data set: 6, 2, 3, 3, 2, 2 - A plumber 3
A plumber can buy plastic pipes in 6-foot and 12-foot lengths. The current job requires eight 4-foot lengths, five 5-foot lengths, and three 7-foot lengths. The plumber wants to figure out how many of each of the two stock lengths should be bought to mini - Dogde Caliber
The petrol kilometers M (unit: kilometers per liter) of the Dodge Caliber car is modeled by the function: M(s) = - 1/28s² + 3s- 31 What is the car's best petrol kilometers, and what speed is attained? - Prove 2
Prove that the minimum number of straight single cuts/strokes needs to divide a given right-angled triangle or an obtuse-angled triangle into a collection of all acute-angled triangles is seven(7). - Lollipop price minimum
Mom bought 6 lollipops for €17. If the cashier rounded up the purchase price to whole euros, what was the least one lollipop could cost? - Cube cuboid minimum Let us have a cube whose edge length is expressed in centimeters and is a natural number. What is the smallest number of such identical cubes that can be made into a cuboid with dimensions of 24 cm, 32 cm, and 60 cm? How long will the edge of these cubes
- Closest point
On the line p: 2x + y + 1 = 0, find the point A ∈ p that is closest to the point P =(1,0) - Container water addition
There are 45 liters of water in a 50-liter container. How many liters of water will it contain if we add another 10 liters of water to it? - Inventory of bottles
Determine the standard inventory of mineral water bottles for smooth operation if the restaurant needs 18,000 half-liter bottles per year. The delivery cycle of goods is 14 days. The minimum insurance stock is set at 5 days. How many liters of mineral wat - Grouped data range
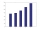In grouped data classes such as 10-15, 16-20, 21-25, 26-30 with the respective frequencies of each class as 3, 5, 4, 3, then the range (range of variation) is: a. 15 b. 6 c. 20 d. 5 - Test grade average
One of the conditions for classification with grade 2 in geography is to obtain an average of at least 64 points from four tests. The minimum number of points a skater must receive from the fourth test to meet this condition is if she received 59, 67, or - Socks
Ben's favorite colors are blue and green. He has six blue socks and six green socks in his sock drawer. Unfortunately, they are completely mixed up, and one day, he has to grab some socks to wear in complete darkness. How many socks (minimum) does he have - Marksman shelter speed
The igniter cord used in normal quarry blasting burns at a rate of 8 mm/s, the length usually used is 60 cm. At what minimum speed must the marksman move to a shelter 150 m away? - The pilot
The pilot is on a mission with 160 liters of fuel. The distance between the main base and the operation area is 2 hours, and between the main base and the backup base is 1 hour. Assume: - Aircraft fuel consumption is 10 lt/h. - The minimum fuel after land
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
