Permutations - practice problems - page 7 of 13
Number of problems found: 260
- Possibilities 38143
If residents of MISSISSIPPI state have to use all the letters to choose their country's name, how many possibilities do they have? - Cups on the shelf
We should place two green, three red, and two yellow cups side by side on the shelf. a) How many different ways of setting up can arise? b) How many different ways of arranging can arise if cups of the same color stand side by side? - Different 38123
How many ways can we put seven different books on the shelf? - Qualifying 37483
There are five good teams in the qualifying group for the World Cup. How many different orders can occur?
- Five-digit 37121
How many different five-digit numbers can we create from digits 4 and 5? - Seedbeds
The father wants to plant two seedbeds of carrots and two seedbeds of onion. Use a tree chart to find how many different options he has for placing the seedbeds. - BRATISLAVA 35531
How many words can we make from all letters of the word BRATISLAVA?
- Different 35501
Dana received four new books. How many different orders can she read them? - 3-digit 35271 How many 3-digit numbers can be created from the digits 1, 2, 3, 4, 5, and 6 if we must not repeat the digits?
- Light bulbs
You are in a room with 3 switches. In the next room, there are 3 switched off classic light bulbs in table lamps, each switch belongs to a light bulb. You cannot see from one room to the other. How do you find out which switch belongs to which light bulb - Number 4 Kamila wrote all-natural numbers from 1 to 400 inclusive. How many times did she write the number 4?
- Double-digit 33471 How many double-digit numbers greater than 60 can we make from digits 0,5,6,7,8,9? The numerals must not be repeated.
- Soccer teams
Have to organize soccer teams. There are three age groups. How many different ways can you organize ten teams for each age group? Is this a permutation or combination? - Competition 33041
The long-term volleyball tournament is played one-on-one. So far, 11 teams have entered the competition. How many matches will be lost when two teams unsubscribe? - Tournament's 32031
Twelve men and four women attended the chess tournament. How many different women's placements can be in the tournament's final table if no two participants have scored the same number of points?
- Wedding guests
Fifteen wedding guests could not agree on who would stand in the wedding photo. The groom suggested that all possible sets of wedding guests be made in the photographs. - School committee
Seven students were elected to the school committee. How many ways can the President, Vice-President, Secretary, and Treasurer be selected? - Participants 31351
How many ways can the first, second, and third prizes be awarded to the 15 participants in the math competition? - Complexity 30631
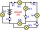Here, you have a task to think about but don't look for great complexity in it. You have 6 bulbs connected here. A to F and 6 switches No. 1 to No. 6. Your task will be to gradually determine which bulbs will always be on if any of the switches are in the - Non-repeating 30101 1. How many different options are there for exchanging a ten-euro bill with one-euro, two-euro, and five-euro bills? a) 5 b) 8 c) 14 d) 10 2. How many non-repeating three-digit numbers can be written using odd digits? a) 999 b) 225 c) 60 d) 25
Do you have unsolved problem that you need help? Ask a question, and we will try to solve it. Solving math problems.
See also our permutations calculator.
