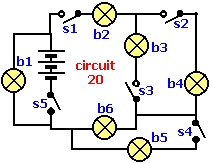
Bulb switch puzzle
Here, you have a task to think about but don't look for great complexity in it. You have 6 bulbs connected here.
A to F and 6 switches No. 1 to No. 6. Your task will be to gradually determine which bulbs will always be on if any of the switches are in the off position.
A to F and 6 switches No. 1 to No. 6. Your task will be to gradually determine which bulbs will always be on if any of the switches are in the off position.
Final Answer:
Tips for related online calculators
See also our permutations calculator.
See also our variations calculator.
Would you like to compute the count of combinations?
See also our variations calculator.
Would you like to compute the count of combinations?
You need to know the following knowledge to solve this word math problem:
combinatoricsbasic operations and conceptsGrade of the word problem
Related math problems and questions:
- Triangle
 Plane coordinates of vertices: K[9, 5] L[-4, 8] M[3, 20] give Triangle KLM. Calculate its area and its interior angles.
Plane coordinates of vertices: K[9, 5] L[-4, 8] M[3, 20] give Triangle KLM. Calculate its area and its interior angles. - An example
 An example is playfully for grade 6 from Math, and I don't know how to explain it to my daughter when I don't want to use the calculator to calculate the cube root. Thus: The student made a cuboid from a block of 16x18x48 mm of plasticine. What will be th
An example is playfully for grade 6 from Math, and I don't know how to explain it to my daughter when I don't want to use the calculator to calculate the cube root. Thus: The student made a cuboid from a block of 16x18x48 mm of plasticine. What will be th - Wagons
 We have six wagons: two white, two blue, and two red. We assemble trains from them; wagons of the same color are exactly the same, so if we change only two white wagons on a train, it's still the same train because I don't know any difference. How many di
We have six wagons: two white, two blue, and two red. We assemble trains from them; wagons of the same color are exactly the same, so if we change only two white wagons on a train, it's still the same train because I don't know any difference. How many di - Diagonals at right angle
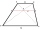 In the trapezoid ABCD, this is given: AB=12cm CD=4cm And diagonals crossed under a right angle. What is the area of this trapezoid ABCD?
In the trapezoid ABCD, this is given: AB=12cm CD=4cm And diagonals crossed under a right angle. What is the area of this trapezoid ABCD? - Family 8
 The father is 38 years old, the daughter is 12, and the son is 14. How many years will a father have as many years as his children together?
The father is 38 years old, the daughter is 12, and the son is 14. How many years will a father have as many years as his children together? - Green - Red
 We have 4 bags. Each consists of one green and 2 red balls. From each, we pull just one ball. What is the probability that we don't pull any green ball?
We have 4 bags. Each consists of one green and 2 red balls. From each, we pull just one ball. What is the probability that we don't pull any green ball? - Fraction to decimal infinite
 Find which digit is at 1000th place after the decimal point in the decimal expansion of the fraction 9/28.
Find which digit is at 1000th place after the decimal point in the decimal expansion of the fraction 9/28.
