Wagons
We have six wagons: two white, two blue, and two red. We assemble trains from them; wagons of the same color are exactly the same, so if we change only two white wagons on a train, it's still the same train because I don't know any difference. How many different trains can we assemble when:
The 1st train must have all six wagons
The 2nd train can have 1 to 6 wagons.
The 1st train must have all six wagons
The 2nd train can have 1 to 6 wagons.
Final Answer:

Tips for related online calculators
See also our combinations with repetition calculator.
Would you like to compute the count of combinations?
See also our permutations calculator.
See also our variations calculator.
Would you like to compute the count of combinations?
See also our permutations calculator.
See also our variations calculator.
You need to know the following knowledge to solve this word math problem:
combinatoricsbasic operations and conceptsnumbersGrade of the word problem
Related math problems and questions:
- Green - Red
 We have 4 bags. Each consists of one green and 2 red balls. From each, we pull just one ball. What is the probability that we don't pull any green ball?
We have 4 bags. Each consists of one green and 2 red balls. From each, we pull just one ball. What is the probability that we don't pull any green ball? - Chess
 How many ways can you select 4 fields on a classic chessboard with 64 fields so that fields don't have the same color?
How many ways can you select 4 fields on a classic chessboard with 64 fields so that fields don't have the same color? - Family 8
 The father is 38 years old, the daughter is 12, and the son is 14. How many years will a father have as many years as his children together?
The father is 38 years old, the daughter is 12, and the son is 14. How many years will a father have as many years as his children together? - Flags
 How many different flags can be made from green, white, blue, red, orange, yellow, and purple materials, so each flag consists of three different colors?
How many different flags can be made from green, white, blue, red, orange, yellow, and purple materials, so each flag consists of three different colors? - Complexity 30631
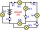 Here, you have a task to think about but don't look for great complexity in it. You have 6 bulbs connected here. A to F and 6 switches No. 1 to No. 6. Your task will be to gradually determine which bulbs will always be on if any of the switches are in the
Here, you have a task to think about but don't look for great complexity in it. You have 6 bulbs connected here. A to F and 6 switches No. 1 to No. 6. Your task will be to gradually determine which bulbs will always be on if any of the switches are in the - The flag
 The flag should consist of 3 different-colored stripes—available colors are white, red, blue, green, and yellow. Specify: A) number of all flags B) number of flags with a blue stripe C) number of flags with a blue stripe in the middle D) the number of fla
The flag should consist of 3 different-colored stripes—available colors are white, red, blue, green, and yellow. Specify: A) number of all flags B) number of flags with a blue stripe C) number of flags with a blue stripe in the middle D) the number of fla - Individual 4688
 The locomotive pulls six wagons. Each of the wagons is either red or blue. The order of colors of individual wagons is the same from the front and back. How many such trains can you draw?
The locomotive pulls six wagons. Each of the wagons is either red or blue. The order of colors of individual wagons is the same from the front and back. How many such trains can you draw?
