Chess
How many ways can you select 4 fields on a classic chessboard with 64 fields so that fields don't have the same color?
Correct answer:
Showing 2 comments:
Mathfun
My attempt Pick 4 out of 64, 635,376 ways
Pick 4 of the same color is 2*32*31*30*29 / 4! = 71,920
Subtract the two is ways not all 4 are same color = 563,456
Pick 4 of the same color is 2*32*31*30*29 / 4! = 71,920
Subtract the two is ways not all 4 are same color = 563,456
Tips for related online calculators
See also our permutations calculator.
See also our variations calculator.
Would you like to compute the count of combinations?
See also our variations calculator.
Would you like to compute the count of combinations?
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Wagons
We have six wagons: two white, two blue, and two red. We assemble trains from them; wagons of the same color are exactly the same, so if we change only two white wagons on a train, it's still the same train because I don't know any difference. How many di - Indistinguishable 48981
How many ways can we build eight indistinguishable towers on an 8 × 8 board so they don't endanger each other? - Transport 7668
The coupon allows you to travel by public transport with a 20% discount cost of 300 CZK. If the ticket costs CZK 20, how often do we have to go after buying coupons so we don't lose out on buying coupons? - Decide 2
Decide whether points A[-2, -5], B[4, 3], and C[16, -1] lie on the same line
- Green - Red
We have 5 bags. Each consists of one green and 2 red balls. From each, we pull just one ball. What is the probability that we don't pull any green ball? - Checkerboard 9091
Determine how many ways we can place 5 different pieces on an 8x8 chessboard so that two are on black squares and three are on white squares. - Complexity 30631
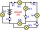Here, you have a task to think about but don't look for great complexity in it. You have 6 bulbs connected here. A to F and 6 switches No. 1 to No. 6. Your task will be to gradually determine which bulbs will always be on if any of the switches are in the
