Right triangle practice problems - page 2 of 86
The Pythagorean theorem which states that in a right triangle, the sum of the squares of the legs (a,b) equals the square of the hypotenuse (c) is a fundamental result in geometry.Number of problems found: 1720
- A tree 3
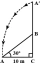 A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree. - A lighthouse
 A lighthouse overlooks a bay, and it is 77 meters high. From the top, the lighthouse keeper can see a yacht southward at an angle of depression of 32 degrees and another boat eastward at an angle of 25 degrees. What is the distance between the boats?
A lighthouse overlooks a bay, and it is 77 meters high. From the top, the lighthouse keeper can see a yacht southward at an angle of depression of 32 degrees and another boat eastward at an angle of 25 degrees. What is the distance between the boats? - In football
 In football, the path that a defender must run to tackle the ball carrier is called the path of pursuit. If the ball carrier runs 40 yards to the end zone and the path of pursuit is 45 yards; how far apart were the ball carrier and defender when they star
In football, the path that a defender must run to tackle the ball carrier is called the path of pursuit. If the ball carrier runs 40 yards to the end zone and the path of pursuit is 45 yards; how far apart were the ball carrier and defender when they star - South and then east
 William walks 16 m south from his house and turns east to walk 63 m to reach his friend's house. While returning, he walks diagonally from his friend's house to reach back to his house. What distance did he walk while returning?
William walks 16 m south from his house and turns east to walk 63 m to reach his friend's house. While returning, he walks diagonally from his friend's house to reach back to his house. What distance did he walk while returning? - A boy 5
 A boy starts at A and walks 3km east to B. He then walks 4km north to C. Find the bearing of C from A.
A boy starts at A and walks 3km east to B. He then walks 4km north to C. Find the bearing of C from A. - A right triangle
 A right triangle has legs with lengths of 24 cm and 21 cm if the length of the hypotenuse, in cm, can be written in the form of 3 sqrt(d), then what is the value of d?
A right triangle has legs with lengths of 24 cm and 21 cm if the length of the hypotenuse, in cm, can be written in the form of 3 sqrt(d), then what is the value of d? - An isosceles triangle
 An altitude is drawn from the vertex of an isosceles triangle, forming a right angle and two congruent triangles. As a result, the altitude cuts the base into two equal segments. The length of the altitude is 18 inches, and the length of the base is 15 in
An altitude is drawn from the vertex of an isosceles triangle, forming a right angle and two congruent triangles. As a result, the altitude cuts the base into two equal segments. The length of the altitude is 18 inches, and the length of the base is 15 in - Building shadow
 When Sun's altitude 30° above the horizontal, then find the length of the shadow of a 50 m high of a building .
When Sun's altitude 30° above the horizontal, then find the length of the shadow of a 50 m high of a building . - Prove 2
 Prove that the minimum number of straight single cuts/strokes needs to divide a given right-angled triangle or an obtuse-angled triangle into a collection of all acute-angled triangles is seven(7).
Prove that the minimum number of straight single cuts/strokes needs to divide a given right-angled triangle or an obtuse-angled triangle into a collection of all acute-angled triangles is seven(7). - A tree 2
 A tree is broken at a height of 6 m from the ground and its top touches the ground at a distance of 8 m from the base of the tree. Find the original height of the tree.
A tree is broken at a height of 6 m from the ground and its top touches the ground at a distance of 8 m from the base of the tree. Find the original height of the tree. - Mrs. Clarke
 Mrs. Clarke is teaching a 5th-grade class. She is standing 40 feet in front of Valeria. Sarah is sitting to Valeria's right. If Sarah and Mrs. Clarke are 50 feet apart, how far apart are Valeria and Sarah?
Mrs. Clarke is teaching a 5th-grade class. She is standing 40 feet in front of Valeria. Sarah is sitting to Valeria's right. If Sarah and Mrs. Clarke are 50 feet apart, how far apart are Valeria and Sarah? - Vertical components
 Find the horizontal and vertical components of the vector which has magnitude 750 as shown in the following figure.
Find the horizontal and vertical components of the vector which has magnitude 750 as shown in the following figure. - FGH right triangle
 Given a right triangle with leg lengths f and g, and hypotenuse h, if f = 7 cm and h = 11.2 cm, what is g?
Given a right triangle with leg lengths f and g, and hypotenuse h, if f = 7 cm and h = 11.2 cm, what is g? - The vertices
 The vertices of a triangle are A (-1,3), B (1,-1), and C (5, 1). Find the length of the median through the vertex C.
The vertices of a triangle are A (-1,3), B (1,-1), and C (5, 1). Find the length of the median through the vertex C. - An equilateral triangle 2
 If the sides of an equilateral triangle are increased by 2 meters, the area is increased by 7√3 square meters. Find the length of the side.
If the sides of an equilateral triangle are increased by 2 meters, the area is increased by 7√3 square meters. Find the length of the side. - A right 3
 A right triangle has a perimeter of 300 cm . its hypotenuse is 130cm. What are the lengths of the other sides .
A right triangle has a perimeter of 300 cm . its hypotenuse is 130cm. What are the lengths of the other sides . - A triangle 10
 A triangle has vertices at (4, 5), (-3, 2), and (-2, 5). What are the coordinates of the vertices of the image after the translation (x, y) arrow-right (x + 3, y - 5)?
A triangle has vertices at (4, 5), (-3, 2), and (-2, 5). What are the coordinates of the vertices of the image after the translation (x, y) arrow-right (x + 3, y - 5)? - Isosceles triangle 17
 One of the equal sides of an isosceles triangle is 13 cm and its perimeter is 50 cm. Find the area of the triangle.
One of the equal sides of an isosceles triangle is 13 cm and its perimeter is 50 cm. Find the area of the triangle. - Isosceles right triangle
 If I have a triangle with a right angle 24 inches long on each side of the right angle what is the length of the third side?
If I have a triangle with a right angle 24 inches long on each side of the right angle what is the length of the third side? - A ladder 2
 A ladder 10 m long reaches the window of a house 8 m above the ground. Find the distance of the foot of the ladder from the base of the wall.
A ladder 10 m long reaches the window of a house 8 m above the ground. Find the distance of the foot of the ladder from the base of the wall.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
