Square root + right triangle - practice problems
Number of problems found: 412
- A right 3
 A right triangle has a perimeter of 300 cm . its hypotenuse is 130cm. What are the lengths of the other sides .
A right triangle has a perimeter of 300 cm . its hypotenuse is 130cm. What are the lengths of the other sides . - An isosceles triangle
 An altitude is drawn from the vertex of an isosceles triangle, forming a right angle and two congruent triangles. As a result, the altitude cuts the base into two equal segments. The length of the altitude is 18 inches, and the length of the base is 15 in
An altitude is drawn from the vertex of an isosceles triangle, forming a right angle and two congruent triangles. As a result, the altitude cuts the base into two equal segments. The length of the altitude is 18 inches, and the length of the base is 15 in - Trigonometric fx
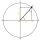 When an acute angle φ is in the standard position, its terminal side passes through point P (1,3). Find trigonometric functions of angle θ : sin φ, cos φ, tan φ, cotan φ.
When an acute angle φ is in the standard position, its terminal side passes through point P (1,3). Find trigonometric functions of angle θ : sin φ, cos φ, tan φ, cotan φ. - FGH right triangle
 Given a right triangle with leg lengths f and g, and hypotenuse h, if f = 7 cm and h = 11.2 cm, what is g?
Given a right triangle with leg lengths f and g, and hypotenuse h, if f = 7 cm and h = 11.2 cm, what is g?
- A lamp
 A lamp shade like that of a frustum has a height of 12 cm and an upper and lower diameter of 10 cm and 20 cm. What area of materials is required to cover the curved surface of the frustum?
A lamp shade like that of a frustum has a height of 12 cm and an upper and lower diameter of 10 cm and 20 cm. What area of materials is required to cover the curved surface of the frustum? - A lighthouse
 A lighthouse overlooks a bay, and it is 77 meters high. From the top, the lighthouse keeper can see a yacht southward at an angle of depression of 32 degrees and another boat eastward at an angle of 25 degrees. What is the distance between the boats?
A lighthouse overlooks a bay, and it is 77 meters high. From the top, the lighthouse keeper can see a yacht southward at an angle of depression of 32 degrees and another boat eastward at an angle of 25 degrees. What is the distance between the boats? - The apothem
 The apothem of a regular hexagon is 5√3 inches. Find one of its sides and area.
The apothem of a regular hexagon is 5√3 inches. Find one of its sides and area. - A right triangle
 A right triangle has legs with lengths of 24 cm and 21 cm if the length of the hypotenuse, in cm, can be written in the form of 3 sqrt(d), then what is the value of d?
A right triangle has legs with lengths of 24 cm and 21 cm if the length of the hypotenuse, in cm, can be written in the form of 3 sqrt(d), then what is the value of d? - The length 17
 The length of one of two chords of a circle is 12cm. If the chords are 6cm and 7cm, respectively, away from the center of the circle, calculate the length of the second chord.
The length of one of two chords of a circle is 12cm. If the chords are 6cm and 7cm, respectively, away from the center of the circle, calculate the length of the second chord.
- Mrs. Clarke
 Mrs. Clarke is teaching a 5th-grade class. She is standing 40 feet in front of Valeria. Sarah is sitting to Valeria's right. If Sarah and Mrs. Clarke are 50 feet apart, how far apart are Valeria and Sarah?
Mrs. Clarke is teaching a 5th-grade class. She is standing 40 feet in front of Valeria. Sarah is sitting to Valeria's right. If Sarah and Mrs. Clarke are 50 feet apart, how far apart are Valeria and Sarah? - The coordinates 3
 The coordinates of two vertices of an equilateral triangle are (1,1) and (5,1). What are the coordinates of the third vertex?
The coordinates of two vertices of an equilateral triangle are (1,1) and (5,1). What are the coordinates of the third vertex? - Triangle 82
 Triangle PQR has vertices located at (2, 2), (5, -4), and (-4, -1). What type of triangle is triangle PQR?
Triangle PQR has vertices located at (2, 2), (5, -4), and (-4, -1). What type of triangle is triangle PQR? - Line segment
 Find the length of the line joining points A(-4,8) and B(-1,4).
Find the length of the line joining points A(-4,8) and B(-1,4). - Quadrilateral 83324
 The volume of a regular quadrilateral pyramid is 72 cm³. Its height is equal to the length of the base edge. Calculate the length of the base and the surface of the pyramid.
The volume of a regular quadrilateral pyramid is 72 cm³. Its height is equal to the length of the base edge. Calculate the length of the base and the surface of the pyramid.
- Equilateral 83322
 The glass weight has the shape of a regular four-sided pyramid with a base edge of 10 cm. The shell walls are equilateral triangles. What is the weight in grams of the paperweight if the density of the glass is 2500kg/m³?
The glass weight has the shape of a regular four-sided pyramid with a base edge of 10 cm. The shell walls are equilateral triangles. What is the weight in grams of the paperweight if the density of the glass is 2500kg/m³? - Quadrilateral 83307
 The diagonal of section DBFH of the regular quadrilateral prism ABCDEFGH inscribes a circle with a diameter of 8 cm. What is the volume of the prism?
The diagonal of section DBFH of the regular quadrilateral prism ABCDEFGH inscribes a circle with a diameter of 8 cm. What is the volume of the prism? - Overhangs 83158
 The area of a right triangle ABC is 346 cm2, and the angle at vertex A is 64°. Calculate the lengths of the overhangs a and b.
The area of a right triangle ABC is 346 cm2, and the angle at vertex A is 64°. Calculate the lengths of the overhangs a and b. - Hypotenuses 83154
 In a right-angled triangle ABC with a right angle at the vertex C, the magnitudes of the hypotenuses are given ta=5, tb=2√10. Calculate the side sizes of triangle ABC and the circle's radius described by this triangle.
In a right-angled triangle ABC with a right angle at the vertex C, the magnitudes of the hypotenuses are given ta=5, tb=2√10. Calculate the side sizes of triangle ABC and the circle's radius described by this triangle. - Horizontal 83148
 The bend has a radius of r = 100 m and is inclined at an angle of 20° to the horizontal plane (= tilt angle). What is the safe (the "best") speed to go through this curve? Sketch the picture regarding NIVS, mark the forces, and calculate.
The bend has a radius of r = 100 m and is inclined at an angle of 20° to the horizontal plane (= tilt angle). What is the safe (the "best") speed to go through this curve? Sketch the picture regarding NIVS, mark the forces, and calculate.
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
