Angle + right triangle - practice problems
Number of problems found: 542
- Know one angle
 In a right-angled triangle, the measure of an angle is 40°. Find the measure of other angles of the triangle in degrees.
In a right-angled triangle, the measure of an angle is 40°. Find the measure of other angles of the triangle in degrees. - An isosceles triangle
 An altitude is drawn from the vertex of an isosceles triangle, forming a right angle and two congruent triangles. As a result, the altitude cuts the base into two equal segments. The length of the altitude is 18 inches, and the length of the base is 15 in
An altitude is drawn from the vertex of an isosceles triangle, forming a right angle and two congruent triangles. As a result, the altitude cuts the base into two equal segments. The length of the altitude is 18 inches, and the length of the base is 15 in - Trigonometric fx
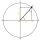 When an acute angle φ is in the standard position, its terminal side passes through point P (1,3). Find trigonometric functions of angle θ : sin φ, cos φ, tan φ, cotan φ.
When an acute angle φ is in the standard position, its terminal side passes through point P (1,3). Find trigonometric functions of angle θ : sin φ, cos φ, tan φ, cotan φ. - A radio antenna
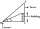 Avanti is trying to find the height of a radio antenna on the roof of a local building. She stands at a horizontal distance of 21 meters from the building. The angle of elevation from her eyes to the roof (point A) is 42°, and the angle of elevation from
Avanti is trying to find the height of a radio antenna on the roof of a local building. She stands at a horizontal distance of 21 meters from the building. The angle of elevation from her eyes to the roof (point A) is 42°, and the angle of elevation from
- A lighthouse
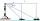 A lighthouse overlooks a bay, and it is 77 meters high. From the top, the lighthouse keeper can see a yacht southward at an angle of depression of 32 degrees and another boat eastward at an angle of 25 degrees. What is the distance between the boats?
A lighthouse overlooks a bay, and it is 77 meters high. From the top, the lighthouse keeper can see a yacht southward at an angle of depression of 32 degrees and another boat eastward at an angle of 25 degrees. What is the distance between the boats? - A boy 5
 A boy starts at A and walks 3km east to B. He then walks 4km north to C. Find the bearing of C from A.
A boy starts at A and walks 3km east to B. He then walks 4km north to C. Find the bearing of C from A. - X-triangle
 Find the length of the x segment in the given triangle drawings.
Find the length of the x segment in the given triangle drawings. - The apothem
 The apothem of a regular hexagon is 5√3 inches. Find one of its sides and area.
The apothem of a regular hexagon is 5√3 inches. Find one of its sides and area. - Angles
 In the triangle ABC, the ratio of angles is α:β = 4:5. The angle γ is 36°. How big are the angles α and β?
In the triangle ABC, the ratio of angles is α:β = 4:5. The angle γ is 36°. How big are the angles α and β?
- Triangle P2
 Can a triangle have two right angles?
Can a triangle have two right angles? - Perpendicular 17423
 According to the map, the scouts were supposed to proceed through the forest perpendicular to its straight edge, where the goal was 3 km away from the starting point. They already deviated from the correct direction by 5° at the start. How far from the ta
According to the map, the scouts were supposed to proceed through the forest perpendicular to its straight edge, where the goal was 3 km away from the starting point. They already deviated from the correct direction by 5° at the start. How far from the ta - Black diamond run
 Taleah is skiing down a black diamond run. She begins skiing at the top of a ski trail whose elevation is about 8625 feet. The ski run ends toward the base of the mountain at 3800 feet. The horizontal distance between these two points is about 4775 feet.
Taleah is skiing down a black diamond run. She begins skiing at the top of a ski trail whose elevation is about 8625 feet. The ski run ends toward the base of the mountain at 3800 feet. The horizontal distance between these two points is about 4775 feet. - Two groves
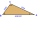 Two groves A B are separated by a forest. Both are visible from the hunting grove C, which is connected to both by direct roads. What will be the length of the projected road from A to B if AC = 5004 m, BC = 2600 m, and angle ABC = 53° 45'?
Two groves A B are separated by a forest. Both are visible from the hunting grove C, which is connected to both by direct roads. What will be the length of the projected road from A to B if AC = 5004 m, BC = 2600 m, and angle ABC = 53° 45'? - Altitude angles
 Cities A, B, and C lie in one elevation plane. C is 50 km east of B, and B is north of A. C is deviated by 50° from A. The plane flies around places A, B, and C at the same altitude. When the aircraft is flying around B, its altitude angle to A is 12°. Fi
Cities A, B, and C lie in one elevation plane. C is 50 km east of B, and B is north of A. C is deviated by 50° from A. The plane flies around places A, B, and C at the same altitude. When the aircraft is flying around B, its altitude angle to A is 12°. Fi
- Powerplant chimney
 From the building window at the height of 7.5 m, we can see the top of the factory chimney at an altitude angle of 76° 30 ′. We can see the chimney base from the same place at a depth angle of 5° 50 ′. How tall is the chimney?
From the building window at the height of 7.5 m, we can see the top of the factory chimney at an altitude angle of 76° 30 ′. We can see the chimney base from the same place at a depth angle of 5° 50 ′. How tall is the chimney? - Observation 82708
 At the top of the hill, there is a 30-meter-high observation tower. We can see its heel and shelter from a certain point in the valley at elevation angles a=28°30" and b=30°40". How high is the top of the hill above the horizontal plane of the observation
At the top of the hill, there is a 30-meter-high observation tower. We can see its heel and shelter from a certain point in the valley at elevation angles a=28°30" and b=30°40". How high is the top of the hill above the horizontal plane of the observation - Horizontally 6296
 The camera with a viewing angle of 120 ° was placed horizontally on the observatory at 30 m. What length d of the section at the tower's base can the camera not capture?
The camera with a viewing angle of 120 ° was placed horizontally on the observatory at 30 m. What length d of the section at the tower's base can the camera not capture? - Two boats
 Two boats are located from a height of 150m above the lake's surface at depth angles of 57° and 39°. Find the distance of both boats if the sighting device and both ships are in a plane perpendicular to the lake's surface.
Two boats are located from a height of 150m above the lake's surface at depth angles of 57° and 39°. Find the distance of both boats if the sighting device and both ships are in a plane perpendicular to the lake's surface. - Measurements 8129
 The plane flies at an altitude of 22.5 km to the observatory. At the time of the first measurement, it was seen at an elevation angle of 28° and during the second measurement at an elevation angle of 50°. Calculate the distance it flies between these two
The plane flies at an altitude of 22.5 km to the observatory. At the time of the first measurement, it was seen at an elevation angle of 28° and during the second measurement at an elevation angle of 50°. Calculate the distance it flies between these two
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
